题目内容
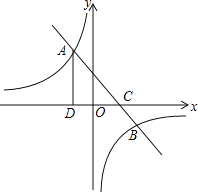
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
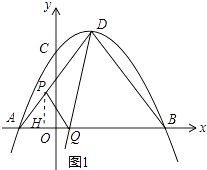
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
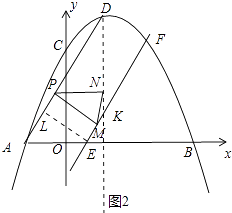
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
【答案】
(1)解:∵a=﹣ ![]() ,抛物线与x轴交与点A(﹣3,0),点B(9,0),
,抛物线与x轴交与点A(﹣3,0),点B(9,0),
∴可以假设抛物线解析式为y=﹣ ![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣ ![]() x2+
x2+ ![]() x+6,
x+6,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+6
x+6
(2)解:∵y=﹣ ![]() x2+
x2+ ![]() x+6=﹣
x+6=﹣ ![]() (x﹣3)2+8,
(x﹣3)2+8,
∴顶点D坐标(3,8),
∵AD=DB=10,
∴∠DAB=∠DBA,
∵PQ∥BD,
∴∠PQA=∠DBA,
∴∠PAQ=∠PQA,
∴PA=PQ,
∴△PAQ为等腰三角形,
作PH⊥AQ于H,则AH=HQ= ![]() (如图1中),
(如图1中),
∴tan∠DAB= ![]() =
= ![]() ,
,
∴PH= ![]() m,
m,
∴S=S△ADQ﹣S△APQ= ![]() m8﹣
m8﹣ ![]() m
m ![]() m=﹣
m=﹣ ![]() m2+4m=﹣
m2+4m=﹣ ![]() (m﹣6)2+12,
(m﹣6)2+12,
∴当m=6时,S最大值=12
(3)解:∵E( ![]() ,0),F(6,6),
,0),F(6,6),
∴直线EF解析式为y= ![]() x﹣2,直线AD解析式为y=
x﹣2,直线AD解析式为y= ![]() x+4,
x+4,
∴EF∥AD,作EL⊥AD于L,(如图2中)
∵AE= ![]() ,sin∠DAB=
,sin∠DAB= ![]() ,
,
∴LE= ![]() ×
× ![]() =
= ![]() =PM,
=PM,
①PM=PN= ![]() 时,
时,
∴xP=3﹣ ![]() =﹣
=﹣ ![]() ,yP=﹣
,yP=﹣ ![]() ×
× ![]() +4=
+4= ![]() ,
,
∴P(﹣ ![]() ,
, ![]() ),
),
∴直线PM解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 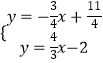 ,解得
,解得 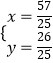 ,
,
∴点M( ![]() ,
, ![]() )
)
∴EM= ![]() =
= ![]() .
.
②NP=NM时,设直线EF与对称轴交于点K,K(3,2),
此时点N在PM的垂直平分线上,DN=NK,
∴N(3,5),P( ![]() ,5),
,5),
∴直线PM的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 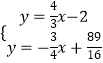 ,解得
,解得 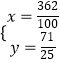 ,
,
∴M( ![]() ,
, ![]() ),
),
∴EM= ![]() =
= ![]() ,
,
③PM=MN时,cos∠MPN= ![]() =
= ![]() ,
,
∴PN= ![]() ,由此可得P(﹣
,由此可得P(﹣ ![]() ,
, ![]() ),
),
∴直线PM解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
由 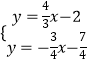 解得
解得 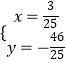 ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
∴EM= ![]() =
= ![]() .
.
综上所述,EM= ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】(1)可以设出抛物线的解析式为y=﹣ ![]() (x+3)(x﹣9)展开即可;(2)作PH⊥AQ于H,则AH=HQ=
(x+3)(x﹣9)展开即可;(2)作PH⊥AQ于H,则AH=HQ= ![]() 根据 S=S△ADQ﹣S△APQ建立二次函数;利用二次函数的性质即可求出结果;(3) 分三种情况讨论①PM=PN,②NP=NM,③PM=MN分别求出直线PM的解析式,利用方程组就出M点的坐标可解决问题。
根据 S=S△ADQ﹣S△APQ建立二次函数;利用二次函数的性质即可求出结果;(3) 分三种情况讨论①PM=PN,②NP=NM,③PM=MN分别求出直线PM的解析式,利用方程组就出M点的坐标可解决问题。
【考点精析】认真审题,首先需要了解解二元一次方程组(二元一次方程组:①代入消元法;②加减消元法),还要掌握二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a)的相关知识才是答题的关键.

【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?