题目内容
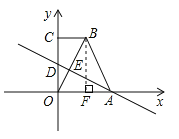
【题目】如图，平面直角坐标系中，
，
，
，
，直线
过
点，且与
轴交于
点．
（1）求点、点
的坐标；
（2）试说明：
；
（3）若点
是直线
上的一个动点，在
轴上是否存在另一个点
，使以
、、、为顶点的四边形是平行四边形？若存在，请直接写出点的坐标；若不存在，请说明理由．
【答案】（1）
；
；（2）见详解；（3）存在，
或
或
【解析】
（1）令
求出x的值，即可得出点A的坐标；作
，可知四边形
是矩形，可得点B的坐标；
（2）先求出点D的坐标，可证
，得出
，进一步可证明结论；
（3）根据平行四边形的对边平行且相等，可得出
再根据点B、M的纵坐标相等，可求得点M的坐标，从而得出BM的值，最后再分情况分析讨论即可得出答案．
解：（1））令，解得：
，点A的坐标为
；
作，四边形是矩形，
∴
∴点B的坐标为
；
（2）令
中x值为0，解得，
，点D的坐标为
，
∴
∵
∴
∴
∵
∴
∴
∴
（3）存在点N．理由如下：
∵点N在x轴上，以
、
、
、
为顶点的四边形是平行四边形
∴
∴点B、M的纵坐标相等
令
解得：
∴
∴
当点N在点O左侧时：点N的坐标为；
当点N在点O右侧时：点N的坐标为；
作点
关于点A对称的点也符合，此时点
的坐标为．
综上所述，点N的坐标为或或．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
