题目内容
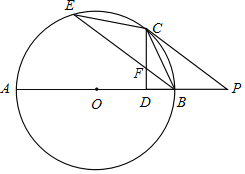
【题目】如图,在矩形ABCD中,AB=6,BC=4,动点Q在边AB上,连接CQ,将△BQC沿CQ所在的直线对折得到△CQN,延长QN交直线CD于点M.
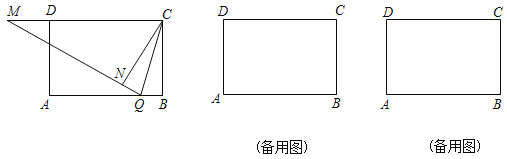
(1)求证:MC=MQ
(2)当BQ=1时,求DM的长;
(3)过点D作DE⊥CQ,垂足为点E,直线QN与直线DE交于点F,且![]() ,求BQ的长.
,求BQ的长.
【答案】(1)见解析;(2)2.5;(3)![]() 或2
或2
【解析】
(1)由矩形的性质得出∠B=90°,AB=CD=6,CD∥AB,得出∠MCQ=∠CQB,由折叠的性质得出△CBQ≌△CNQ,求出BC=NC=4,NQ=BQ=1,∠CNQ=∠B=90°,∠CQN=∠CQB,得出∠CNM=90°,∠MCQ=∠CQN,证出MC=MQ.
(2)设DM=x,则MQ=MC=6+x,MN=5+x,在Rt△CNM中,由勾股定理得出方程,解方程即可.
(3)分两种情况:①当点M在CD延长线上时,由(1)得:∠MCQ=∠CQM,证出∠FDM=∠F,得出MD=MF,过M作MH⊥DF于H,则DF=2DH,证明△MHD∽△CED,得出![]() ,求出MD=
,求出MD=![]() CD=1,MC=MQ=7,由勾股定理得出MN即可解决问题.
CD=1,MC=MQ=7,由勾股定理得出MN即可解决问题.
②当点M在CD边上时,同①得出BQ=2即可.
(1)证明:∵四边形ABCD是矩形,
∴DC∥AB
即∠MCQ=∠CQB,
∵△BQC沿CQ所在的直线对折得到△CQN,
∴∠CQN=∠CQB,
即∠MCQ=∠MQC,
∴MC=MQ.
(2)∵四边形ABCD是矩形,△BQC沿CQ所在的直线对折得到△CQN,
∴∠CNM=∠B=90°,
设DM=x,则MQ=MC=6+x,MN=5+x,
在Rt△CNM中,MB2=BN2+MN2,
即(x+6)2=42+(x+5)2,
解得:x=![]() ,
,
∴DM=![]() ,
,
∴DM的长2.5.
(3)解:分两种情况:
①当点M在CD延长线上时,如图所示: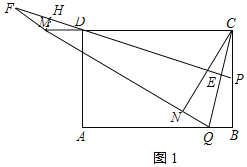
由(1)得∠MCQ=∠MQC,
∵DE⊥CQ,
∴∠CDE=∠F,
又∵∠CDE=∠FDM,
∴∠FDM=∠F,
∴MD=MF.
过M点作MH⊥DF于H,则DF=2DH,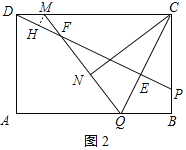
又![]() ,
,
∴![]() ,
,
∵DE⊥CQMH⊥DF,
∴∠MHD=∠DEC=90°,
∴△MHD∽△DEC
∴![]() ,
,
∴DM=1,MC=MQ=7,
∴MN=![]()
∴BQ=NQ=![]()
②当点M在CD边上时,如图所示,类似可求得BQ=2.
综上所述,BQ的长为![]() 或2.
或2.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?