题目内容
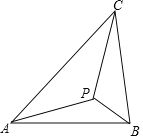
【题目】如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A.5 B.4 C.3+![]() D.2+
D.2+![]()
【答案】D.
【解析】
试题分析:如图,在等腰直角三角形△DEF中,∠EDF=90°,DE=DF,∠1=∠2=∠3,
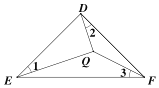
∵∠1+∠QEF=∠3+∠DFQ=45°,∴∠QEF=∠DFQ,∵∠2=∠3,
∴△DQF∽△FQE,∴![]() ,
,
∵DQ=1,∴FQ=![]() ,EQ=2,∴EQ+FQ=2+
,EQ=2,∴EQ+FQ=2+![]() ,
,
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯 | 电量 | 电价 |
一档 | 0~180度 | 0.6元/度 |
二档 | 181~400度 | 二档电价 |
三档 | 401度及以上 | 三档电价 |