Question

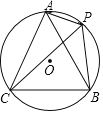
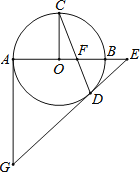
【题目】如图，在△ABC中，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且AC＝CF，∠CBF＝∠CFB．

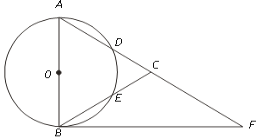
（1）求证：直线BF是⊙O的切线；

（2）若点D，点E分别是弧AB的三等分点，当AD=5时，求BF的长和扇形DOE的面积；

（3）在（2）的条件下，如果以点C为圆心，r为半径的圆上总存在不同的两点到点O的距离为5，则r的取值范围为 ．

Answer 1

【答案】（1）见解析；（2），；（3）＜r＜

【解析】

（1）证明：∵∠CBF＝∠CFB ∴CB＝CF

又∵AC＝CF∴CB＝AC＝CF

∴以C为圆心AC长为半径的⊙C过A、B、F

∴∠ABF＝90°

∴直线BF是⊙O的切线．

（2）解：连接DO，EO，

∵点D，点E分别是弧AB的三等分点

∴∠AOD＝60°

又∵OA＝OD

∴△AOD是等边三角形

∴∠OAD＝60°，AB=10

在Rt△ABF中，∠ABF＝90°,∠BAF＝60°, AB=10

∴BF＝

（3）连接OC圆心距OC＝，圆O半径r=5．

∴＜r＜