题目内容
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B,C的坐标分别为(4,0)和(0,4),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
(1)求抛物线和直线AD的解析式;
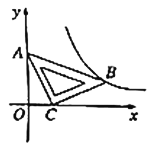
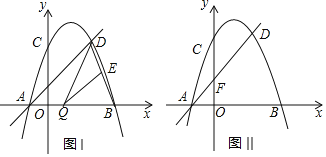
(2)如图Ⅰ,点Q是线段AB上一动点,过点Q作QE∥AD,交BD于点E,连接DQ,求△QED面积的最大值;
(3)如图Ⅱ,直线AD交y轴于点F,点M,N分别是抛物线对称轴和抛物线上的点,若以C,F,M,N为顶点的四边形是平行四边形,求点M的坐标.
【答案】(1)y=﹣![]() x2+x+4,y=x+2;(2)△QED面积的最大值是3;(3)点M的坐标为(1,
x2+x+4,y=x+2;(2)△QED面积的最大值是3;(3)点M的坐标为(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() ).
).
【解析】
(1)待定系数法得到抛物线的解析式为y=﹣![]() x2+x+4;直线AD的解析式为y=x+2;
x2+x+4;直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),根据相似三角形的性质得到EG=![]() ,
,
∴S△QDE=S△BDQ﹣S△BEQ=![]() ×(4﹣m)×4﹣
×(4﹣m)×4﹣![]() (4﹣m)×
(4﹣m)×![]() =﹣
=﹣![]() m2+
m2+![]() m+
m+![]() ,根据二次函数的性质可求△QED面积的最大值;
,根据二次函数的性质可求△QED面积的最大值;
(3)分两种情况讨论①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,于是可求点M的坐标;
②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,求出点P、N的坐标后可求点M的坐标.
解:(1)根据题意得,
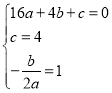 ,
,
解得: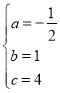 ,
,
∴抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
∵B(4,0),对称轴为x=1,
∴A(﹣2,0),
∵D(2,m)在抛物线的解析式y=﹣![]() x2+x+4上,
x2+x+4上,
∴点D的坐标是D(2,4),
设直线AD的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),
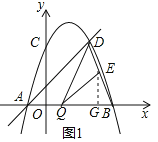
∵QE∥AD,
∴△BEQ∽△BDA,
∴![]() ,
,
即![]() ,
,
解得:EG=![]() ,
,
∴S△BEQ=![]() ×(4﹣m)×
×(4﹣m)×![]() ,
,
∴S△QDE=S△BDQ﹣S△BEQ=![]() ×(4﹣m)×4﹣
×(4﹣m)×4﹣![]() (4﹣m)×
(4﹣m)×![]() =﹣
=﹣![]() m2+
m2+![]() m+
m+![]() =﹣
=﹣![]() (m﹣1)2+3,
(m﹣1)2+3,
∴当m=1时,△QED面积取得最大值等于3;
(3)∵直线AD交y轴于点F,
∴F(0,2),
∵抛物线的解析式是y=﹣![]() x2+x+4上,
x2+x+4上,
∵抛物线的顶点坐标(1,![]() ),
),
①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,此时,MN=CF=2,
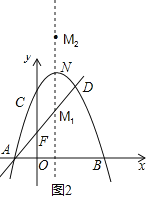
∴点M的坐标(1,![]() ),(1,
),(1,![]() );
);
②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,
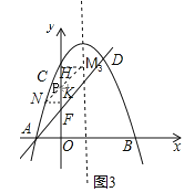
过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,
易得△MHP≌△NKP,P(0,3)
∴点M,N的横坐标分别是1,﹣1,
∴N(﹣1,![]() ),
),
∴PK=3-![]() =
=![]() =HP,
=HP,
∴HO=3+![]() =
=![]() ,
,
∴M(1,![]() ),
),
综上所述,点M的坐标为:(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() ).
).

 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
观察表格:根据表格解答下列问题:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
(2)在下图的直角坐标系中画出函数![]() 的图象,并根据图象,直接写出当
的图象,并根据图象,直接写出当![]() 取什么实数时,不等式
取什么实数时,不等式![]() 成立;
成立;
(3)该图象与![]() 轴两交点从左到右依次分别为
轴两交点从左到右依次分别为![]() 、
、![]() ,与
,与![]() 轴交点为
轴交点为![]() ,求过这三个点的外接圆的半径.
,求过这三个点的外接圆的半径.