题目内容
【题目】如图,相距2cm的两个点A、B在直线l上.它们分别以2cm/s和1cm/s的速度在l上同时向右平移,当点A,B分别平移到点A1 , B1的位置时,半径为1cm的⊙A1 , 与半径为BB1的⊙B相切.则点A平移到点A1 , 所用的时间为s. ![]()
【答案】![]() 或3
或3
【解析】解:设点A平移到点A1 , 所用的时间为ts, 根据题意得:AB=2cm,AA1=2tcm,A1B=(2﹣2t)cm,BB1=tcm,
如图,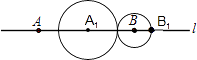
此时外切:2﹣2t=1+t,
∴t= ![]() ;
;
如图,此时内切:2﹣2t=1﹣t,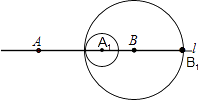
∴t=1,此时两圆心重合,舍去;
或2﹣2t=t﹣1,
解得:t=1,此时两圆心重合,舍去;
如图,此时内切:2t﹣t+1=2,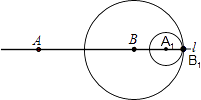
∴t=1,此时两圆心重合,舍去;
如图:此时外切:2t﹣t﹣1=2,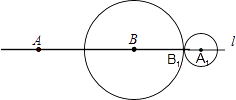
∴t=3.
∴点A平移到点A1 , 所用的时间为1(此时两圆重合,舍去)或3s.
所以答案是: ![]() 或3.
或3.
【考点精析】通过灵活运用圆与圆的位置关系,掌握两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.即可以解答此题.

【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试,计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,达到9分或10分为优秀,成绩如表1所示,并制作了成绩分析表(表2)
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | a | 3.82 | 70% | 30% |
二班 | b | c | 10 | 4.94 | 80% | 40% |
(1)求表2中,a,b,c;
(2)有人说二班的及格率、优秀率均高于一班,所以二班成绩比一班成绩好;但也有人坚定认为一班成绩比二班成绩好.请你给出支持一班成绩好的两条理由.