题目内容

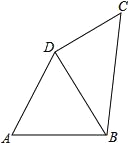
【题目】如图，在四边形ABCD中，AB=AD=8，∠A=60°，∠ADC=150°，四边形ABCD的周长为32．

（1）求∠BDC的度数；

（2）四边形ABCD的面积．

【答案】（1）90°；（2）24+16

【解析】

（1）先根据题意得出△ABD是等边三角形，△BCD是直角三角形，进而可求出∠BDC的度数；

（2）根据四边形周长计算BC，CD，即可求△BCD的面积，正△ABD的面积根据计算公式计算，即可求得四边形ABCD的面积为两个三角形的面积的和．

（1）∵AB=AD=8cm，∠A=60°，∴△ABD是等边三角形．

∵∠ADC=150°，∴∠BDC=150°﹣60°=90°；

（2）∵△ABD为正三角形，AB=8cm，∴其面积为××AB×AD=16．

∵BC+CD=32﹣8﹣8=16，且BD=8，BD2+CD2=BC2，解得：BC=10，CD=6，∴直角△BCD的面积=×6×8=24，故四边形ABCD的面积为24+16．

练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠ACB=90°，以BC为半径作⊙B，交AB于点D，交AB的延长线于点E，连接CD、CE．
（1）求证：△ACD∽△AEC；
（2）当 = 时，求tanE；
（3）若AD=4，AC=4 ，求△ACE的面积．

【题目】（1）如图①，已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

（2）如图②，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

【题目】如图，在△ABC中，∠B=40°，∠C=80°，AD是BC边上的高，AE平分∠BAC．

（1）求∠BAE的度数；（2）求∠DAE的度数．

【题目】在三角形ABC中，D是边BC上的一点，已知AC=5，AD=6，BD=10，CD=5，那么三角形ABC的面积是（　　）

A. 30 B. 36 C. 72 D. 125

【题目】如图，在平面直角坐标系xOy中，边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上，二次函数y=﹣ x2+bx+c的图象经过B、C两点．

（1）求该二次函数的解析式；
（2）结合函数的图象探索：当y＞0时x的取值范围．

【题目】如图，AD是△ABC的中线，tanB= ，cosC= ，AC= ．求：
（1）BC的长；
（2）sin∠ADC的值．

【题目】如图，在四边形ABCD中，∠BAD=∠C=90°，AB=AD=9，AE⊥BC于E，AE=8，则CD的长为_____．

【题目】如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE

（1）请判断：AF与BE的数量关系是 ， 位置关系是 .
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予说明
（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网