题目内容
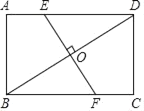
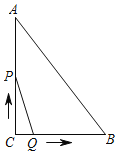
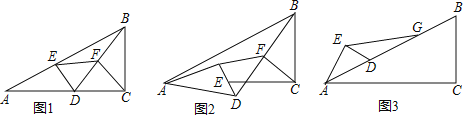
【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,连接AF、DC.
(1)求证:四边形ADCF是平行四边形;
(2)若AC=BC,判断四边形ADCF的形状,无需说明理由;
(3)若∠ACB=90°,判断四边形ADCF的形状,无需说明理由.
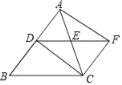
【答案】(1)详见解析;(2)四边形ADCF是矩形;(3)四边形ADCF是菱形.
【解析】
(1)可先证得△AED≌△CEF,可证得ED=EF,可证明四边形ADCF为平行四边形;
(2)证明四边形ADCF是平行四边形,再得出AC=DF即可.
(3)根据DF∥BC,证明AC⊥DF即可.
(1)证明:∵DE是△ABC的中位线,
∴E为AC中点,
∴AE=EC,
∵CF∥BD,
∴∠ADE=∠DFC,
在△ADE和△CFE中,
∵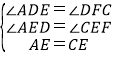 ,
,
∴△ADE≌△CFE(AAS),
∴DE=FE
∴四边形ADCF是平行四边形.
(2)解:四边形ADCF是矩形.
理由:∵DE=FE,AE=AC,
∴四边形ADCF是平行四边形,
∴AD=CF,
∵AD=BD,
∴BD=CF,又因为BD∥CF
∴四边形DBCF为平行四边形,
∴BC=DF,
∵AC=BC,
∴AC=DF,
∴平行四边形ADCF是矩形.
(3)解:四边形ADCF是菱形.
理由:∵DF∥BC,
∴∠AED=∠ACB=90°,
∴AC⊥DF,
∵四边形ADCF是平行四边形,
∴四边形ADCF是菱形.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?