题目内容
已知:如图,E,F在AC上,AD//CB且AD=CB,∠D=∠B.求证:AE=CF.

证明:∵AD∥CB,
∴∠A=∠C,
∵AD=CB,∠D=∠B
∴△ADF≌△CBE(ASA)
∴AF=CE
∴AF+EF=CE+EF
∴AE="CF"
∴∠A=∠C,
∵AD=CB,∠D=∠B
∴△ADF≌△CBE(ASA)
∴AF=CE
∴AF+EF=CE+EF
∴AE="CF"
根据两直线平行内错角相等即可得出∠A=∠C,再根据全等三角形的判定即可判断出△ADF≌△CBE,得出AF=CE,进而得出AE=CF.

练习册系列答案
相关题目


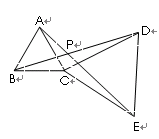
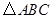 中,
中,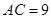 ,点
,点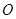 在
在 上,且
上,且 ,点
,点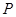 是
是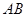 上一动点,连结
上一动点,连结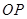 ,将线段
,将线段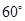 得到线段
得到线段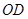 .要使点
.要使点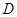 恰好落在
恰好落在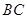 上,则
上,则 的长是___________________
的长是___________________
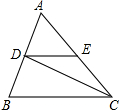
 中,
中, ,点
,点 在
在 上,
上, 垂直平分
垂直平分 ,垂足为点
,垂足为点 ,且
,且 ,则
,则 .
. 
