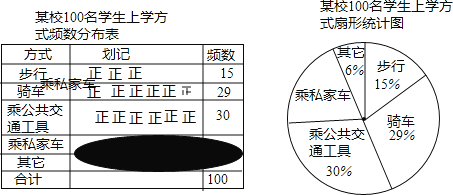
��Ŀ����
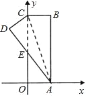
����Ŀ����ͼ����OΪֱ��AB��һ�㣬����O������OC��ʹ![]() .��һ����
.��һ����![]() �ǵ�ֱ�����ǰ�OMN��һ��������ڵ�O����б��OM��ֱ��AB�غϣ���������ֱ�DZ�ON��MN����ֱ��AB���·�.
�ǵ�ֱ�����ǰ�OMN��һ��������ڵ�O����б��OM��ֱ��AB�غϣ���������ֱ�DZ�ON��MN����ֱ��AB���·�.

��1����ͼ1�е����ǰ�OMN���ŵ�O��ʱ����ת![]() ����ͼ2��ʾ������OM�Ƿ�ƽ��
����ͼ2��ʾ������OM�Ƿ�ƽ��![]() ����˵�����ɣ�
����˵�����ɣ�
��2����ͼ2�е����ǰ�OMN�Ƶ�O��ʱ�������ת��ͼ3��λ����ʾ��ʹ��ON��![]() ���ڲ�����̽��
���ڲ�����̽��![]() ��
��![]() ֮���������ϵ����˵�����ɣ�
֮���������ϵ����˵�����ɣ�
��3����ͼ1�е����ǰ�OMN�Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ�DZ�ON����ֱ��ǡ��ƽ�����
���ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ�DZ�ON����ֱ��ǡ��ƽ�����![]() ����t��ֵΪ________��ֱ��д�������.
����t��ֵΪ________��ֱ��д�������.
���𰸡���1��OMƽ��![]() �����ɼ���������2��
�����ɼ���������2��![]() �����ɼ���������3��9���81��
�����ɼ���������3��9���81��
��������
��1��������ת�����ʿɵá�BOM�Ķ�����Ȼ������MOC�Ķ����ж�OM�Ƿ�ƽ�֡�CON��
��2�����á�AOM=45��-��AON�͡�NOC=45��-��AON���жϡ�AOM���CON֮���������ϵ��
��3��ON��ת22.5�Ⱥ�202.5��ʱ��ONƽ�֡�AOC��Ȼ�������ٶȹ�ʽ����t��ֵ��
�⣺��1��OMƽ��![]() ��
��
�������£�
��֪![]() ����ΪOM��ת
����ΪOM��ת![]() ��
��
����![]() ��
��
����![]() ��
��
��![]() ��
��
����OMƽ��![]() .
.
��2��![]()
�������£�
��Ϊ![]() ��
��
����![]() ��
��
��Ϊ![]() ��
��
����![]() ��
��
����![]() .
.
��3��9���81��. �������£�
T=![]() ��45���2.5��=9���룩��t=��180��+22.5�㣩��2.5��=81���룩��
��45���2.5��=9���룩��t=��180��+22.5�㣩��2.5��=81���룩��
�ʴ�Ϊ9���81��.��