题目内容
【题目】定义:给定两个不等式组![]() 和
和![]() ,若不等式组
,若不等式组![]() 的任意一个解,都是不等式组
的任意一个解,都是不等式组![]() 的一个解,则称不等式组
的一个解,则称不等式组![]() 为不等式组
为不等式组![]() 的“子集”。例如:不等式组:
的“子集”。例如:不等式组:![]() 是:
是:![]() 的“子集”。
的“子集”。
(1)若不等式组:![]() ,
,![]() ,则其中不等式组 是不等式组
,则其中不等式组 是不等式组![]() 的“子集”(填
的“子集”(填![]() 或
或![]() );
);
(2)若关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,则
的“子集”,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() ,
,![]() ,
,![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,下列三个不等式组:
,下列三个不等式组:![]() ,
,![]() ,
,![]() 满足:
满足:![]() 是
是![]() 的“子集”且
的“子集”且![]() 是
是![]() 的“子集”,求
的“子集”,求![]() 的值;
的值;
(4)已知不等式组![]() 有解,且是不等式组
有解,且是不等式组![]() 的“子集”,则满足条件的有序整数对
的“子集”,则满足条件的有序整数对![]() 共有多少个?
共有多少个?
【答案】(1)A;(2)a≥2;(3)-4;(4)10.
【解析】
(1)先分别求出不等组A,B的解集,再根据不等式组子集的定义进行判断即可.
(2)先求出不等式组![]() 的解集为x>2,再根不等组子集的定义,可得不等式组
的解集为x>2,再根不等组子集的定义,可得不等式组![]() 的解集在x>2的内部,故a≥2.
的解集在x>2的内部,故a≥2.
(3)先根据子集的定义求出a=3,b=4,c=2,d=5.代入式子求解即可.
(4)先根据子集的定义确定出m,n的取值范围,再由它均为整数,从而确定出有序整数对![]() 共有10个.
共有10个.
解:(1)∵![]() ,
,
∴A的解集为:3<x<6.
∵![]() ,
,
∴B的解集为x>1.
∵![]() ,
,
∴M的解集为x>2.
∴A是M的子集.
故答案为:A.
(2)∵不等式组![]() 的解集为x>2,且关于
的解集为x>2,且关于![]() 的不等式组
的不等式组![]() 是不等式组
是不等式组![]() 的“子集”,
的“子集”,
∴![]() 的取值范围是a≥2.
的取值范围是a≥2.
故答案为:a≥2.
(3)∵![]() 是
是![]() 的“子集”,
的“子集”,
∴c≤a≤b≤d.
∵![]() ,
,![]() ,
,![]() ,
,![]() 为互不相等的整数,其中
为互不相等的整数,其中![]() ,
,![]() ,
,
∴c<![]() <d.
<d.
∵![]() 是
是![]() 的“子集”,
的“子集”,
∴1< c<![]() <d<6.
<d<6.
∴a=3,b=4,c=2,d=5.
∴![]() =3-4+2-5=-4.
=3-4+2-5=-4.
(4)∵不等式组![]() 有解,
有解,
∴不等式组M的解集为![]() ≤x≤
≤x≤![]() ,
,
∵不等式组![]() 是不等式组
是不等式组![]() 的“子集”,
的“子集”,
∴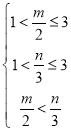 ,
,
解得: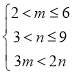 ,
,
∵m,n为整数,
∴足条件的有序整数对![]() 共有10个,它们分别是(3,5)、(3,6)、(3,7)、(3,8)、(3,9)、(4,7)、(4,8)、(4,9)、(5,8)、(5,9).
共有10个,它们分别是(3,5)、(3,6)、(3,7)、(3,8)、(3,9)、(4,7)、(4,8)、(4,9)、(5,8)、(5,9).

 计算高手系列答案
计算高手系列答案