题目内容
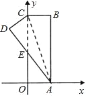
【题目】如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点E的坐标_____.
【答案】(0,![]() )
)
【解析】
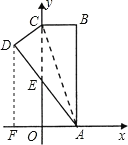
首先过D作DF⊥AO于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=1,设OE=x,那么CE=3-x,DE=x,利用勾股定理即可求出OE的长度,即可求出点E的坐标.
如图,过D作DF⊥AO于F,
∵点B的坐标为(1,3),
∴BC=AO=1,AB=OC=3,
根据折叠可知:CD=BC=OA=1,AD=AB=3,![]()
在△CDE和△AOE中,
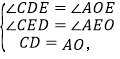
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,AE=CE,
设OE=x,那么CE=3x,DE=x,
∴在Rt△DCE中,![]()
∴![]()
∴![]()
∴![]()
点E的坐标为:![]()
故答案为:![]()

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目