题目内容
【题目】已知,等腰Rt△ABC,在直角边AB的左侧作直线AP,点B关于直线AP的对称点为E,连结BE,CE,其中CE交直线AP于点F.
(1)当∠PAB=29°时,求∠ACE的度数.
(2)当0°<∠PAB<45°时,利用(图1),求∠BEC度数.
(3)若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.


【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,证明见解析
,证明见解析
【解析】
(1)由轴对称的性质和等腰三角形的性质得出∠EAP=∠PAB=29°,得出∠EAC=148°,证出AE=AC,由等腰三角形的性质和三角形内角和定理即可得出结果;
(2)由(1)得:∠EAP=∠PAB,∠AEC=∠ACE,由三角形内角和定理即可得出结论;
(3)作CG⊥AP于G,由AAS证明△ACG≌△BAM,得出CG=AM,证出点A是△BCE的外接圆圆心,由圆周角定理得出![]() ,得出△EFM和△CFG是等腰直角三角形,由勾股定理即可得出结论.
,得出△EFM和△CFG是等腰直角三角形,由勾股定理即可得出结论.
(1)由轴对称的性质可得:AE=AB,BM=EM,AM⊥BE,∠AME=∠BMA=90°,
∴∠EAP=∠PAB=29°,
∴∠EAC=90°+2×29°=148°,
∵△ABC是等腰直角三角形,
∴AB=AC,
∴AE=AC,
∴![]() ;
;
(2)由(1)得:∠EAP=∠PAB,∠AEC=∠ACE,
∵∠AEC+∠ACE+∠EAC=180°,
∴∠AEC+∠ACE+2∠EAP =90°
即2∠AEC +2∠EAP =90°
∴∠EAP +∠AEC =45°
∴∠EFM =45°
∴∠BEC =45°;
(3)如图2所示:作CG⊥AP于G
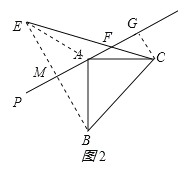
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,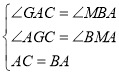 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点![]() 是
是![]() 的外接圆圆心,
的外接圆圆心,
∴![]() ,
,
∴![]() ,
,
∴![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.

【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .