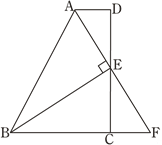
题目内容
【题目】如图,A、B、C是直线l上的三个点,∠DAB=∠DBE=∠ECB=a,且BD=BE.
(1)求证:AC=AD+CE;
(2)若a=120°,点F在直线l的上方,△BEF为等边三角形,补全图形,请判断△ACF的形状,并说明理由.

【答案】(1)详见解析;(2)△ACF为等边三角形.
【解析】
(1)由外角的性质可得∠ADB=∠CBE,由“AAS”可得△ADB≌△CBE,可得AD=CB,AB=CE,可得结论;
(2)由“SAS”可证△AFB≌△CFE,可得AF=CF,∠AFB=∠CFE,可得∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°,可得△ACF是等边三角形.
证明:(1)∵∠DAB=∠DBE=α,
∴∠ADB+∠ABD=∠CBE+∠ABD=180°﹣α.
∴∠ADB=∠CBE
在△ADB和△CBE中,
∵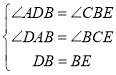 ,
,
∴△ADB≌△CBE(AAS)
∴AD=CB,AB=CE.
∴AC=AB+BC=AD+CE
(2)补全图形.
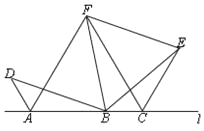
△ACF为等边三角形.
理由如下:
∵△BEF为等边三角形,
∴BF=EF,∠BFE=∠FBE=∠FEB=60°.
∵∠DBE=120°,∴∠DBF=60°.
∵∠ABD=∠CEB(已证),
∴∠ABD+∠DBF=∠CEB+∠FEB,
即∠ABF=∠CEF.
∵AB=CE(已证),
∴△AFB≌△CFE(SAS),
∴AF=CF,∠AFB=∠CFE.
∴∠AFC=∠AFB+∠BFC=∠CFE+∠BFC=60°.
∴△ACF为等边三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
项目品种 | 单价(元/棵) | 成活率 |
A | m | 91% |
B | 100 | 97% |
(1)求表中m的值;
(2)预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?