题目内容
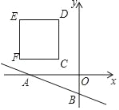
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
x﹣1分别交x轴、y轴于点A、B,在第二象限内有一边长为2的正方形CDEF,已知C(﹣1,1),若动点P从C出发以每秒1个单位的速度沿着正方形CDEF的边逆时针运动一周(到达C点后停止运动),设P点运动的时间为t秒.
(1)是否存在t,使得以P为圆心,![]() 为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
为半径的圆与直线AB相切?若存在,求出所有t的值;若存在,请说明理由.
(2)在点P运动的同时,直线AB以每秒1个单位的速度向右作匀速运动(与点P同时停止)是否存在t,使得以P为圆心,![]() 为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
为半径的圆与平移后的直线A′B′相切?请直接写出所有t的值.
【答案】(1)满足条件的t的值为1或4.(2)满足条件的t的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 设存在点P.作PH⊥AB,PM⊥x轴交AB于Q,可证△PHQ∽△AOB,可得PQ=![]() ,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
,分点P在CD上时,与当点P在DE上时讨论,可得t的值;
(2)由题意平移后可得直线A′B′的解析式为,作PH⊥A′B′,PM⊥x轴交A′B′于Q.当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,分①当点P在CD上时,②当点P在DE上时,
,分①当点P在CD上时,②当点P在DE上时,
③当点P在EF上时,三种情况讨论,可的t的值.
解:(1)假设存在点P.作PH⊥AB,PM⊥x轴交AB于Q.

∵PQ∥y轴,
∴∠OBA=∠PQH,
∵∠AOB=∠PHQ=Rt∠,
∴△PHQ∽△AOB,
∴![]() =
=![]() ,
,
∵A(﹣1,2)或(﹣3,3),PH=![]() ,
,
∴AO=2,AB=![]() ,
,
∴PQ=![]() ,
,
①当点P在CD上时,t+1+![]() =
=![]() ,解得t=1,
,解得t=1,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1]=
(1﹣t)﹣1]=![]() ,解得t=4,此时点P与E重合.
,解得t=4,此时点P与E重合.
综上所述,满足条件的t的值为1或4.
(2)由题意平移后的直线A′B′的解析式为y=﹣![]() x﹣1+
x﹣1+![]() ,
,
作PH⊥A′B′,PM⊥x轴交A′B′于Q.
当PH=![]()
![]() 时,同法可得PQ=
时,同法可得PQ=![]() ,
,
①当点P在CD上时,1+t﹣(![]() ﹣1+
﹣1+![]() )=
)=![]() ,解得t=
,解得t=![]() ,
,
②当点P在DE上时,3﹣[﹣![]() (1﹣t)﹣1+
(1﹣t)﹣1+![]() ]=
]=![]() ,解得t=
,解得t=![]() ,
,
③当点P在EF上时,![]() ﹣1+
﹣1+![]() ﹣(6﹣t+1)=
﹣(6﹣t+1)=![]() ,解得t=
,解得t=![]() ,
,
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() .
.