题目内容
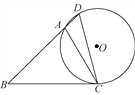
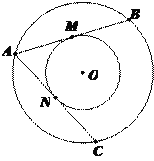
【题目】如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.
【答案】(1)证明见解析;(2)S圆环=16π
【解析】试题分析:(1)连结OM、ON、OA由切线长定理可得AM=AN,由垂径定理可得AM=BM,AN=NC,从而可得AB=AC.
(2)由垂径定理可得AM=BM=4,由勾股定理得OA2-OM2=AM 2=16,代入圆环的面积公式求解即可.
(1)证明:连结OM、ON、OA
∵AB、AC分别切小圆于点M、N.
∴AM=AN,OM⊥AB,ON⊥AC,
∴AM=BM,AN=NC,
∴AB=AC
(2)解:∵弦AB切与小圆⊙O相切于点M
∴OM⊥AB
∴AM=BM=4
∴在Rt△AOM中,OA2-OM2=AM 2=16
∴S圆环=πOA2-πOM2=πAM 2=16π

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目