题目内容
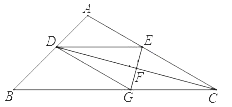
【题目】如图,△ABC中,CD平分∠ACB,CD的垂直平分线分别交AC、DC、BC
于点E、F、G,连接DE、DG.
(1)求证:四边形DGCE是菱形;
(2)若∠ACB=30°,∠B=45°,CG=10,求BG的长.
【答案】(1)证明见解析;(2)BG= 5+5![]() .
.
【解析】
(1)由角平分线的性质和中垂线性质可得∠EDC=∠DCG=∠ACD=∠GDC,可得CE∥DG,DE∥GC,DE=EC,可证四边形DGCE是菱形;
(2)过点D作DH⊥BC,由锐角三角函数可求DH的长,GH的长,BH的长,即可求BG的长.
(1)∵CD平分∠ACB,
∴∠ACD=∠DCG
∵EG垂直平分CD,
∴DG=CC,DE=EC
∴∠DCG=∠GDC,∠ACD=∠EDC
∴∠EDC=∠DCG=∠ACD=∠GDC
∴CE∥DG,DE∥GC
∴四边形DECG是平行四边形
又∵DE=EC
∴四边形DGCE是菱形
(2)如图,过点D作DH⊥BC,
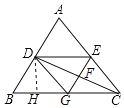
∵四边形DGCE是菱形,
∴DE=DG=GC=10,DG∥EC
∴∠ACB=∠DGB=30°,且DH⊥BC
∴DH=5,HG=![]() DH=5
DH=5![]()
∵∠B=45°,DH⊥BC
∴∠B=∠BDH=45°
∴BH=DH=5
∴BG=BH+HG=5+5![]()

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目