题目内容
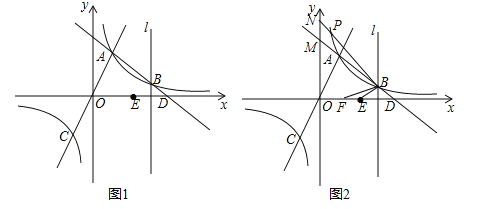
【题目】如图1,一次函数y=﹣x+b与反比例函数![]() (k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数
(k≠0)的图象交于点A(1,3),B(m,1),与x轴交于点D,直线OA与反比例函数![]() (k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.
(k≠0)的图象的另一支交于点C,过点B作直线l垂直于x轴,点E是点D关于直线l的对称点.

(1)k= ;
(2)判断点B、E、C是否在同一条直线上,并说明理由;
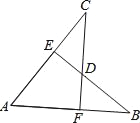
(3)如图2,已知点F在x轴正半轴上,OF=![]() ,点P是反比例函数
,点P是反比例函数![]() (k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
(k≠0)的图象位于第一象限部分上的点(点P在点A的上方),∠ABP=∠EBF,则点P的坐标为( , ).
【答案】(1)3;(2)在同一直线上;(3)![]() ,
, ![]() .
.
【解析】试题分析:(1)把A点坐标代入![]() 中可求出k的值;
中可求出k的值;
(2)先利用反比例函数的中心对称性得到C(﹣1,﹣3),再把B(m,1)代入![]() 求出m得到B(3,1),通过确定直线AB的解析式得到D(4,0),接着利用对称性确定E(2,0),于是利用待定系数法看球出直线BC的解析式为y=x﹣2,然后判断点E是否直线BC上;
求出m得到B(3,1),通过确定直线AB的解析式得到D(4,0),接着利用对称性确定E(2,0),于是利用待定系数法看球出直线BC的解析式为y=x﹣2,然后判断点E是否直线BC上;
(3)直线AB交y轴于M,直线BP交y轴于N,如图2,先确定M(0,4),计算出BM=![]() ,BE=
,BE=![]() ,EF=
,EF=![]() ,再证明△BMN∽△BEF,通过相似比计算出MN=
,再证明△BMN∽△BEF,通过相似比计算出MN=![]() ,从而得到N(0,
,从而得到N(0, ![]() ),则利用待定系数法得到直线BN的解析式为
),则利用待定系数法得到直线BN的解析式为![]() ,然后通过解方程组
,然后通过解方程组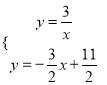 得P点坐标.
得P点坐标.
试题解析:解:(1)∵A(1,3)在反比例函数![]() 的图象上,∴k=1×3=3;
的图象上,∴k=1×3=3;
(2)点B、E、C在同一条直线上.理由如下:
∵直线OA与反比例函数![]() (k≠0)的图象的另一支交于点C,∴点A与点C关于原点对称,∴C(﹣1,﹣3),∵B(m,1)在反比例函数
(k≠0)的图象的另一支交于点C,∴点A与点C关于原点对称,∴C(﹣1,﹣3),∵B(m,1)在反比例函数![]() 的图象上,∴1×m=3,解得m=3,即B(3,1),把A(1,3)代入y=﹣x+b得﹣1+b=3,解得b=4,∴直线AB的解析式为y=﹣x+4,当y=0时,﹣x+4=0,解得x=4,则D(4,0),∵点E与点D关于直线x=3对称,∴E(2,0),设直线BC的解析式为y=px+q,把B(3,1),C(﹣1,﹣3)代入得:
的图象上,∴1×m=3,解得m=3,即B(3,1),把A(1,3)代入y=﹣x+b得﹣1+b=3,解得b=4,∴直线AB的解析式为y=﹣x+4,当y=0时,﹣x+4=0,解得x=4,则D(4,0),∵点E与点D关于直线x=3对称,∴E(2,0),设直线BC的解析式为y=px+q,把B(3,1),C(﹣1,﹣3)代入得: ![]() ,解得:
,解得: ![]() ,∴直线BC的解析式为y=x﹣2,当x=2时,y=x﹣2=0,∴点E在直线BC上,即点B、E、C在同一条直线上;
,∴直线BC的解析式为y=x﹣2,当x=2时,y=x﹣2=0,∴点E在直线BC上,即点B、E、C在同一条直线上;
(3)直线AB交y轴于M,直线BP交y轴于N,如图2,当x=0时,y=﹣x+4=4,则M(0,4),而B(3,1),E(2,0),F(![]() ,0),∴BM=
,0),∴BM=![]() =
=![]() ,BE=
,BE=![]() =
=![]() ,EF=2﹣
,EF=2﹣![]() =
=![]() ,∵OM=OD=4,∴△OMD为等腰直角三角形,∴∠OMD=∠ODM=45°,∵点E与点D关于直线x=3对称,∴∠BED=∠BDE=45°,∴∠BMN=∠BEF=135°,∵∠ABP=∠EBF,∴△BMN∽△BEF,∴
,∵OM=OD=4,∴△OMD为等腰直角三角形,∴∠OMD=∠ODM=45°,∵点E与点D关于直线x=3对称,∴∠BED=∠BDE=45°,∴∠BMN=∠BEF=135°,∵∠ABP=∠EBF,∴△BMN∽△BEF,∴![]() ,即
,即 ,解得MN=
,解得MN=![]() ,∴N(0,
,∴N(0, ![]() ),设直线BN的解析式为y=ax+n,把B(3,1),N(0,
),设直线BN的解析式为y=ax+n,把B(3,1),N(0, ![]() )代入得:
)代入得: 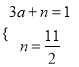 ,解得:
,解得: 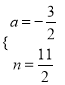 ,∴直线BN的解析式为
,∴直线BN的解析式为![]() ,解方程组
,解方程组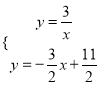 ,得:
,得: ![]() 或
或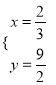 ,∴P点坐标为(
,∴P点坐标为(![]() ,
, ![]() ).
).
故答案为:3, ![]() ,
, ![]() .
.