��Ŀ����
����Ŀ����ͼ1����ֱ֪��PQ��MN����A��ֱ��PQ�ϣ���C��D��ֱ��MN�ϣ�����AC��AD����PAC=50�㣬��ADC=30�㣬AEƽ�֡�PAD��CEƽ�֡�ACD��AE��CE�ཻ��E�� 
��1�����AEC�Ķ�����
��2������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ2��ʾλ�ã���ʱA1Eƽ�֡�AA1D1 �� CEƽ�֡�ACD1 �� A1E��CE�ཻ��E����PAC=50�㣬��A1D1C=30�㣬���A1EC�Ķ����� 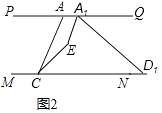
��3������ͼ1�е��߶�AD��MN����ƽ�Ƶ�A1D1��ͼ3��ʾλ�ã����������루2����ͬ�����ʱ��A1EC�Ķ����� 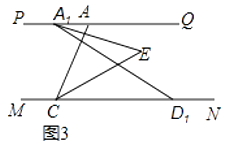
���𰸡�
��1���⣺��ͼ1��ʾ��
��ֱ��PQ��MN����ADC=30�㣬
���ADC=��QAD=30�㣬
���PAD=150�㣬
�ߡ�PAC=50�㣬AEƽ�֡�PAD��
���PAE=75�㣬
���CAE=25�㣬
�ɵá�PAC=��ACN=50�㣬
��CEƽ�֡�ACD��
���ECA=25�㣬
���AEC=180�㩁25�㩁25��=130�㣻
��2���⣺��ͼ2��ʾ��
�ߡ�A1D1C=30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1=30�㣬
���PA1D1=150�㣬
��A1Eƽ�֡�AA1D1��
���PA1E=��EA1D1=75�㣬
�ߡ�PAC=50�㣬PQ��MN��
���CAQ=130�㣬��ACN=50�㣬
��CEƽ�֡�ACD1��
���ACE=25�㣬
���CEA1=360�㩁25�㩁130�㩁75��=130�㣻
��3���⣺��ͼ3��ʾ������E��FE��PQ��

�ߡ�A1D1C=30�㣬�߶�AD��MN����ƽ�Ƶ�A1D1��PQ��MN��
���QA1D1=30�㣬
��A1Eƽ�֡�AA1D1��
���QA1E=��2=15�㣬
�ߡ�PAC=50�㣬PQ��MN��
���ACN=50�㣬
��CEƽ�֡�ACD1��
���ACE=��ECN=��1=25�㣬
���CEA1=��1+��2=15��+25��=40��
����������1��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���CAE�Լ���ECA�Ķ����������ó��𰸣���2��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���CAE�Լ���ECA�Ķ����������ó��𰸣���3��ֱ�����ý�ƽ���ߵ����ʽ��ƽ���ߵ����ʵó���1�͡�2�Ķ����������ó��𰸣�
�����㾫����������Ҫ������ƽ���ߵ����ʺ�ƽ�Ƶ����ʵ����֪ʶ�㣬��Ҫ������ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ������پ���ƽ��֮���ͼ����ԭ����ͼ�εĶ�Ӧ�߶�ƽ�У�����ͬһֱ���ϣ�����ȣ���Ӧ����ȣ�ͼ�ε���״���С��û�з����仯���ھ���ƽ�ƺ�Ӧ���������߶�ƽ�У�����ͬһֱ���ϣ�����Ȳ�����ȷ�����⣮