题目内容
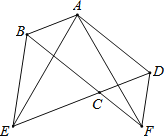
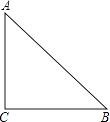
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数. 
请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB()
所以∠DCE=∠B()
又因为∠B=95°,
所以∠DCE=°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB==°,
因为DC∥AB
所以∠DCA=∠CAB,()
所以∠DCA=°.
【答案】同旁内角互补,两直线平行;两直线平行,同位角相等;95;∠CAD;25;两直线平行,内错角相等;25
【解析】解:∵∠DAB+∠D=180°,
∴DC∥AB(同旁内角互补,两直线平行),
∴∠DCE=∠B(两直线平行,同位角相等).
又∵∠B=95°,
∴∠DCE=95°;
∵AC平分∠DAB,∠CAD=25°,
∴∠CAB=∠CAD=25°,
∵DC∥AB
∴∠DCA=∠CAB,(两直线平行,内错角相等),
∴∠DCA=25°.
所以答案是:同旁内角互补,两直线平行;两直线平行,同位角相等;95;∠CAD,25;两直线平行,内错角相等;25.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目