题目内容
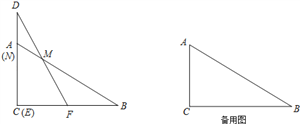
【题目】如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，△ABC的面积是28cm2 ， AB=16cm，AC=12cm，求DE的长． 
【答案】解：∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC， ∴DE=DF，
∵S△ABC=S△ABD+S△ACD= 
AB×DE+ AC×DF，
∴S△ABC= （AB+AC）×DE，
即 ×（16+12）×DE=28，
解得DE=2（cm）．
【解析】根据角平分线上的点到角的两边距离相等可得DE=DF，再根据S△ABC=S△ABD+S△ACD列方程计算即可得解．
【考点精析】本题主要考查了角平分线的性质定理的相关知识点，需要掌握定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上才能正确解答此题．
练习册系列答案
相关题目
【题目】已知二次函数y＝ax2＋bx＋c中x和y的值如下表：( )
x | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
y | -5.6 | -3.1 | -1.5 | 0.9 | 1.8 |
则ax2＋bx＋c=0的一个根的范围是( )
A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14
