Question

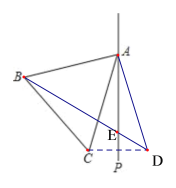
【题目】如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E．

（1）依题意补全图形；

（2）若∠PAC＝20°，求∠AEB的度数；

Answer 1

【答案】（1）见详解；（2）60°

【解析】

（1）作出点C关于直线AP的对称点为点D，连接AD，BD，即可得到所作图形；

（2）由等边三角形的性质和轴对称的性质，可得AB=AD，∠BAD=100°，结合三角形内角和定理，求出∠ADB的度数，然后由三角形外角的性质，即可求解．

（1）补全图形，如图所示：

（2）∵点C关于直线AP的对称点为点D，

∴AC=AD，∠PAD=∠PAC＝20°，

∵三角形ABC是等边三角形，

∴AB=AC，∠BAC=60°，

∴AB=AD，∠BAD=60°+20°+20°=100°，

∴∠ADB=（180°-100°）÷2=40°，

∴∠AEB=∠ADB+∠PAD=40°+20°=60°．