题目内容
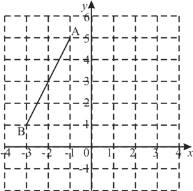
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣1,5),点B的坐标为(﹣3,1).
(1)在平面直角坐标系中作线段AB关于y轴对称的线段A1B1(A与A1,B与B1对应);
(2)求△AA1B1的面积;
(3)在y轴上存在一点P,使PA+PB的值最小,则点P的坐标为________.
【答案】(1)见解析;(2)4;(3)(0,4)
【解析】
(1)利用关于y轴对称的点的坐标特征写出点A1、B1的坐标,然后描点、连线即可;
(2)根据三角形面积公式计算即可;
(3)连接AB1交y轴于点P,则点P就是所求的点,根据图形得出坐标即可.
(1)如图:
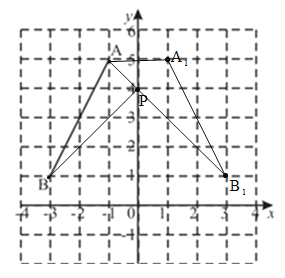
(2)∵A(-1,5),A1(1,5),
∴AA1=2,
∴△AA1B1的面积=![]() ;
;
(3)连接AB1交y轴于点P,则P(0,4)就是所求的点.

练习册系列答案
相关题目







