题目内容
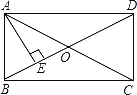
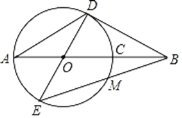
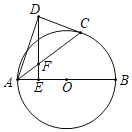
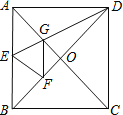
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,点E,F分别在AB,BD上,且△ADE≌△FDE,DE交AC于点G,连接GF.得到下列四个结论:①∠ADG=22.5°;②S△AGD=S△OGD;③BE=2OG;④四边形AEFG是菱形,其中正确的结论是_____.(填写所有正确结论的序号)
【答案】①③④
【解析】
由正方形的性质及△ADE≌△FDE,可判断①;
证明△ADG≌△FDG(SAS),可判断②;
通过全等三角形的性质及等腰三角形的判定可证得EF=GF=EA=GA,从而判定四边形AEFG是菱形,故④可判断;
由△OGF为等腰直角三角形及△BFE为等腰直角三角形,可判断③.
解:∵四边形ABCD是正方形,
∴∠GAD=∠ADO=45°,
∴由△ADE≌△FDE,
可得:∠ADG=![]() ∠ADO=22.5°,
∠ADO=22.5°,
故①正确;
∵△ADE≌△FDE,
∴AD=FD,∠ADG=∠FDG,
又∵GD=GD,
∴△ADG≌△FDG(SAS),
∴S△AGD>S△OGD,
故②错误;
∵△ADE≌△FDE,
∴EA=EF,
∵△ADG≌△FDG,
∴GA=GF,∠AGD=∠FGD,
∴∠AGE=∠FGE.
∵∠EFD=∠AOF=90°,
∴EF∥AC,
∴∠FEG=∠AGE,
∴∠FGE=∠FEG,
∴EF=GF,
∴EF=GF=EA=GA,
∴四边形AEFG是菱形,故④正确;
∵四边形AEFG是菱形,
∴AE∥FG,
∴∠OGF=∠OAB=45°,
∴△OGF为等腰直角三角形,
∴FG=![]() OG,
OG,
∴EF=![]() OG,
OG,
∵△BFE为等腰直角三角形,
∴BE=![]() EF=
EF=![]()
![]()
![]() OG=2OG,
OG=2OG,
∴③正确.
综上,正确的有①③④.
故答案为:①③④.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目