Question

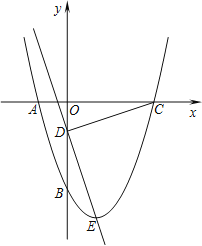
【题目】如图，AC为⊙O的直径，B为AC延长线上一点，且∠BAD＝∠ABD＝30°，BC＝1，AD为⊙O的弦，连结BD，连结DO并延长交⊙O于点E，连结BE交⊙O于点M．

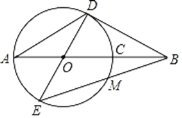
（1）求证：直线BD是⊙O的切线；

（2）求⊙O的半径OD的长；

（3）求线段BM的长．

Answer 1

【答案】（1）证明见解析；（2）⊙O的半径OD的长为1；（3）线段BM的长为

【解析】

（1）利用等腰三角形的性质及三角形的内角和求得∠ODB＝90°，按照切线的判定定理可得答案；

（2）利用30°角所对的直角边等于斜边的一半及圆的半径相等可得答案；

（3）先由勾股定理求得BE的长，再连接DM，利用有两个角相等的三角形相似可判定△BMD∽△BDE，然后利用相似三角形的性质可得比例式，从而求得答案．

解：（1）证明：∵OA＝OD，∠BAD＝∠ABD＝30°，

∴∠BAD＝∠ADO＝30°，

∴∠DOB＝∠BAD+∠ADO＝60°，

∴∠ODB＝∠180°﹣∠DOB﹣∠ABD＝90°，

∵OD为⊙O的半径，

∴直线BD是⊙O的切线；

（2）∵∠ODB＝90°，∠ABD＝30°，

∴OD＝OB，

∵OC＝OD，

∴BC＝OC＝1，

∴⊙O的半径OD的长为1；

（3）∵OD＝1，

∴DE＝2，BD＝，

∴BE＝

如图，连接DM，

∵DE为⊙O的直径，

∴∠DME＝90°，

∴∠DMB＝90°，

∵∠EDB＝90°，

∴∠EDB＝∠DME，

又∵∠DBM＝∠EBD，

∴△BMD∽△BDE，

∴

∴BM＝

∴线段BM的长为