题目内容
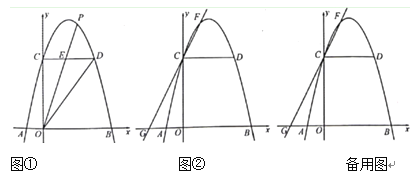
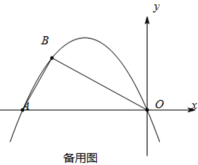
【题目】如图,在平面直角坐标系中,O是坐标原点,抛物线![]() 经过A(-5,0),
经过A(-5,0),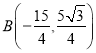 两点,连接AB,BO.
两点,连接AB,BO.
(1)求抛物线表达式;
(2)点C是第三象限内的一个动点,若△AOC与△AOB全等,请直接写出点C坐标______;
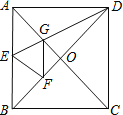
(3)若点D从点O出发沿线段OA向点A作匀速运动,速度为每秒1个单位长度,同时线段OA上另一个点H从点A出发沿线段AO向点O作匀速运动,速度为每秒2个单位长度(当点H到达点O时,点D也同时停止运动).过点D作x轴的垂线,与直线OB交于点E,延长DE到点F,使得EF=DE,以DF为边,在DF左侧作等边三角形DGF(当点D运动时,点G、点F也随之运动).过点H作x轴的垂线,与直线AB交于点L,延长HL到点M,使得LM=HL,以HM为边,在HM的右侧作等边三角形HMN(当点H运动时,点M、点N也随之运动).当点D运动t秒时,△DGF有一条边所在直线恰好过△HMN的重心,直接写出此刻t的值.

【答案】(1)![]() ;(2)
;(2)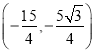 ,
,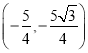 ;(3)1或
;(3)1或![]() .
.
【解析】
(1)利用待定系数法求二次函数的解析式;
(2)先根据勾股定理的逆定理证明![]() 是直角三角形,且
是直角三角形,且![]() ,当
,当![]() 与
与![]() 全等,如图1,分两种情况:由对称性可得点
全等,如图1,分两种情况:由对称性可得点![]() 的坐标;
的坐标;
(3)分两种情况:
①当直线![]() 经过
经过![]() 的重心
的重心![]() 时,如图2,先根据特殊的三角函数值计算
时,如图2,先根据特殊的三角函数值计算![]() ,根据
,根据![]() ,列方程
,列方程![]() ,可得
,可得![]() 的值;②当直线
的值;②当直线![]() 经过
经过![]() 的重心
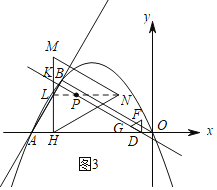
的重心![]() 时,如图3,根据平行线分线段成比例定理可得结论.
时,如图3,根据平行线分线段成比例定理可得结论.
解:(1)把![]() ,
,![]() ,
,![]() 两点代入抛物线
两点代入抛物线![]() 中得:
中得:
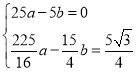 ,
,
解得: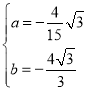 ,
,
![]() ;
;
(2)如图1,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,且
是直角三角形,且![]() ,
,
当![]() 与
与![]() 全等,如图1,分两种情况:
全等,如图1,分两种情况:

①在![]() 轴的上方,由对称得:
轴的上方,由对称得:![]() ,
,![]() ;
;
②在![]() 轴的下方,同理得:
轴的下方,同理得:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
综上,点![]() 的坐标是
的坐标是![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() ;
;
(3)分两种情况:
①当直线![]() 经过
经过![]() 的重心
的重心![]() 时,如图2,
时,如图2,
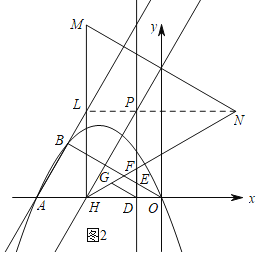
连接![]() ,
,
![]() ,且
,且![]() 是等边三角形,
是等边三角形,
![]() 在
在![]() 上,
上,
由题意得:![]() ,
,![]() ,
,
由(2)知:![]() ,
,![]() ,
,
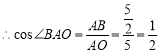 ,
,
![]() ,
,
![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() 是重心,
是重心,
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ;
;
②当直线![]() 经过
经过![]() 的重心
的重心![]() 时,如图3,
时,如图3,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
解得:![]() ,
,
综上,![]() 的值是
的值是![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

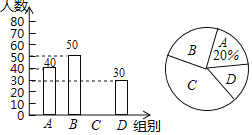
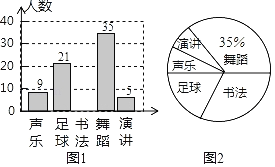
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | 0.35 |
一般 | m | |
不好 | 36 |
请根据图表中提供的信息,解答下列问题:
(1)本次抽样共调查了 名学生;
(2)m= ;
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.