题目内容
 10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是
10、如图,已知Rt△ABC中,∠C=90°∠A=36°,以C为圆心,CB为半径的圆交AB于P,则弧BP的度数是72
°.分析:连CP,由∠C=90°∠A=36°,根据互余求得∠B=90°-36°=54°,又根据等腰三角形的性质得∠CPB=∠B=54°,再根据三角形的内角和定理得到∠PCB=180°-54°-54°=72°,最后根据圆心角的度数等于它所对的弧的度数得到即可弧BP的度数.
解答:解:连CP,如图,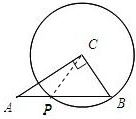
∵∠C=90°∠A=36°,
∴∠B=90°-36°=54°,
又∵CB=CP,
∴∠CPB=∠B=54°,
∴∠PCB=180°-54°-54°=72°,
∴弧BP的度数=72°.
故答案为72.

∵∠C=90°∠A=36°,
∴∠B=90°-36°=54°,
又∵CB=CP,
∴∠CPB=∠B=54°,
∴∠PCB=180°-54°-54°=72°,
∴弧BP的度数=72°.
故答案为72.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了三角形的内角和定理以及圆心角的度数等于它所对的弧的度数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.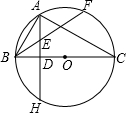 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠CAB=30°,BC=5.过点A做AE⊥AB,且AE=15,连接BE交AC于点P. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为