Question

【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A(3，0)，顶点B在y轴正半轴上，顶点D在x轴负半轴上，若抛物线y=－x2－5x+c经过点B、C，则菱形ABCD的面积为（ ）

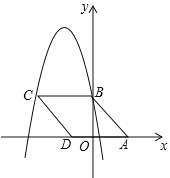
A.15B.20C.25D.30

Answer 1

【答案】B

【解析】

根据抛物线的解析式结合抛物线过点B、C，即可得出点C的横坐标，由菱形的性质可得出AD=AB=BC=5，再根据勾股定理可求出OB的长度，套用平行四边形的面积公式即可得出菱形ABCD的面积．

解：抛物线的对称轴为，

∵抛物线y=-x2-5x+c经过点B、C，且点B在y轴上，BC∥x轴，
∴点C的横坐标为-5．
∵四边形ABCD为菱形，
∴AB=BC=AD=5，
∴点D的坐标为（-2，0），OA=3．
在Rt△ABC中，AB=5，OA=3，

∴OB=，

∴S菱形ABCD=ADOB=5×4=20．
故选：B．