题目内容
【题目】在ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F,且BE=DF.
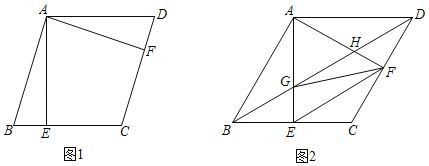
(1)如图1,求证:ABCD是菱形;
(2)如图2,连接BD,交AE于点G,交AF于点H,连接EF、FG,若∠CEF=30°,在不添加任何字母及辅助线的情况下,请直接写出图中面积是△BEG面积2倍的所有三角形.
【答案】(1)见解析;(2)△ABG、△ADH、△AGH、△DFG
【解析】
(1)证明△AEB≌△AFD得出AB=AD,即可得出结论;
(2)连接AC交BD于O,则AC⊥BD,证出EF∥BD,得出∠CBD=∠CEF=30°,∠ABC=60°,证明△ABC是等边三角形,∠EBG=∠FDH,得出∠BAG=∠ABG,∴AG=BG,同理:AH=DH,得出BE=![]() BC=
BC=![]() AB,由菱形的性质和角平分线的性质得出点G到AB与BC边上的高相等,得出S△ABG=2S△BEG;证明△BEG≌△DFH得出BG=DH,得出AG=AH,得出S△ABG=S△ADH,S△ADH=2S△BEG;证出△AGH是等边三角形,得出GH=AG=AH=BG=DH,OG=
AB,由菱形的性质和角平分线的性质得出点G到AB与BC边上的高相等,得出S△ABG=2S△BEG;证明△BEG≌△DFH得出BG=DH,得出AG=AH,得出S△ABG=S△ADH,S△ADH=2S△BEG;证出△AGH是等边三角形,得出GH=AG=AH=BG=DH,OG=![]() AG=EG,OA=
AG=EG,OA=![]() OG=BE,得出△AGH的面积=2△BEG的面积;△GHF的面积=△DFH的面积,得出△DFG的面积=2△BEG的面积.
OG=BE,得出△AGH的面积=2△BEG的面积;△GHF的面积=△DFH的面积,得出△DFG的面积=2△BEG的面积.
解:(1)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△AEB和△AFD中, ,
,
∴△AEB≌△AFD(ASA),
∴AB=AD,
∴ABCD是菱形;
(2)解:图中面积是△BEG面积2倍的所有三角形为△ABG、△ADH、△AGH、△DFG;理由如下:
连接AC交BD于O,如图所示:
则AC⊥BD,
∵BC=CD,BE=DF,
∴BE:BC=DF:CD,
∴EF∥BD,
∴∠CBD=∠CEF=30°,
∴∠ABC=60°,
∵ABCD是菱形,
∴BC=CD=AB,
∴△ABC是等边三角形,∠EBG=∠FDH,
∴∠BAG=∠ABG,
∴AG=BG,
同理:AH=DH,
∵AE⊥BC,
∴BE=![]() BC=
BC=![]() AB,
AB,
∵ABCD是菱形,
∴BD是∠ABC的平分线,
∴点G到AB与BC边上的高相等,
∴S△ABG=2S△BEG,
在△BEG和△DFH中, ,
,
∴△BEG≌△DFH(ASA),
∴△BEG的面积=△DFH的面积,BG=DH,
∴AG=AH,
∵△AEB≌△AFD,
∴S△ABG=S△ADH,∴S△ADH=2S△BEG;
∵∠GAH=∠OAG+∠OAH=60°,
∴△AGH是等边三角形,
∴GH=AG=AH=BG=DH,OG=![]() AG=EG,OA=
AG=EG,OA=![]() OG=BE,
OG=BE,
∴△AGH的面积=2△BEG的面积,
∴△GHF的面积=△DFH的面积,
∴△DFG的面积=2△BEG的面积;
∴图中面积是△BEG面积2倍的三角形为:△ABG、△ADH、△AGH、△DFG.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案