题目内容
【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,右下表是调控后的价目表.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?

【答案】⑴ 20元;9.5吨;⑵10.25吨;⑶ 11月交16元、12月交36元或11月交36元、12月交16元.
【解析】
试题(1)因为用水量为8 吨,所以计算单价分为两段,列式计算即可;先计算用水量为6吨和10吨的总价,与26对比,发现9月份用水量x的取值范围,从而列出方程求解;
(2)由题意得出水费30元,用水量超过了10吨,列方程求未知数即可;
(3)设该户居民11月用水量为x吨,12月用水量为(18-x)吨;共交水费52元.列方程求解即可.
试题解析:(1)6×2+(8-6)×4=20,
答:该用户8月应交水费20元;
设该用户9月份用水量为x吨,
2×6=12,2×6+(10-6)×4=28,
∵12<26<28,
∴6<x<10,
则6×2+4(x-6)=26,
x=9.5,
答:该用户9月份用水量为9.5吨;
(2)该用户10月份用水量为y吨,则y>10,
根据题意得:6×2+(10-6)×4+8(y-10)=30,
y=10.25;
(3)设11月份用水x吨,12月份用水y吨,
①当11月份用水不超过6吨时,12月份用水超过10吨时,由题意得:
![]()
解得:![]() (舍去)
(舍去)
②当11月份用水超过6吨不超过10时,12月份用水超过10吨时,由题意得:
![]()
解得:![]()
故11月份的水费为:6×2+1×4=16(元);
12月份的水费为:6×2+4×4+1×8=36(元);
同理可得:11月交36元、12月交16元.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成). 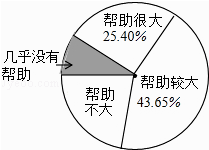
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1)