题目内容
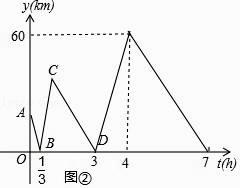
【题目】如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示. 
(1)M、N两地之间的距离为km;
(2)求线段BC所表示的y与t之间的函数表达式;
(3)若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象.
【答案】
(1)80
(2)解:由题意可知B( ![]() ,0),C(1,40),
,0),C(1,40),
设y与x之间的函数表达式为y=kx+b.
根据题意得,
当x= ![]() 时,y=0;
时,y=0;
当x=1时,y=40.
所以 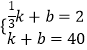 ,
,
解得 ![]() .
.
所以,y与x之间的函数表达式为y=60x﹣20
(3)解:如图所示:
故答案为:80.
【解析】解:(1)20×3+20 =60+20
=80(km).
答:M、N两地之间的距离为80km;
(1)根据路程=速度×时间,可求PM,再计算20即可求解;(2)由题意可知B( ![]() ,0),C(1,40),根据待定系数法可求线段BC所表示的y与t之间的函数表达式;(3)当甲开汽车返回M地时,甲,乙两人之间的距离y(km)最大为60;依此补全函数图象.
,0),C(1,40),根据待定系数法可求线段BC所表示的y与t之间的函数表达式;(3)当甲开汽车返回M地时,甲,乙两人之间的距离y(km)最大为60;依此补全函数图象.

练习册系列答案
相关题目