题目内容
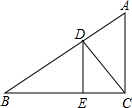 如图,∠B=∠ACD,∠B+∠BCD=90°,DE⊥BC,垂足为E.
如图,∠B=∠ACD,∠B+∠BCD=90°,DE⊥BC,垂足为E.
(1)AC与DE平行吗?为什么?
(2)∠B与∠CDE相等吗?为什么?
(1)解:AC∥DE,
理由是:∵∠B=∠ACD,∠B+∠BCD=90°,
∴∠ACD+∠BCD=90°,
即∠ACB=90°,
∵DE⊥BC,
∴∠DEB=90°=∠ACB,
∴AC∥DE.
(2)解:∠B=∠CDE,
理由是:∵AC∥DE,
∴∠CDE=∠ACD,
∵∠B=∠ACD,
∴∠B=∠CDE.
分析:(1)求出∠ACB=∠DEB=90°,根据平行线的判定定理即可推出答案;
(2)根据平行线的性质推出∠CDE=∠ACD,根据已知即可推出结论.
点评:本题考查了平行线的性质和判定,垂线等知识点的应用,能熟练地运用平行线的性质和判定进行推理是解此题的关键,主要培养学生分析问题和解决问题的能力.
理由是:∵∠B=∠ACD,∠B+∠BCD=90°,
∴∠ACD+∠BCD=90°,
即∠ACB=90°,
∵DE⊥BC,
∴∠DEB=90°=∠ACB,
∴AC∥DE.
(2)解:∠B=∠CDE,
理由是:∵AC∥DE,
∴∠CDE=∠ACD,
∵∠B=∠ACD,
∴∠B=∠CDE.
分析:(1)求出∠ACB=∠DEB=90°,根据平行线的判定定理即可推出答案;
(2)根据平行线的性质推出∠CDE=∠ACD,根据已知即可推出结论.
点评:本题考查了平行线的性质和判定,垂线等知识点的应用,能熟练地运用平行线的性质和判定进行推理是解此题的关键,主要培养学生分析问题和解决问题的能力.

练习册系列答案
相关题目
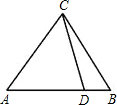 如图,若△ACD∽△ABC,以下4个等式错误的是( )
如图,若△ACD∽△ABC,以下4个等式错误的是( )A、
| ||||
B、
| ||||
| C、CD2=AD•DB | ||||
| D、AC2=AD•AB |
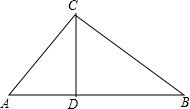 如图,如果△ACD∽△ABC,那么下列各式中成立的是( )
如图,如果△ACD∽△ABC,那么下列各式中成立的是( )| A、CD2=AD•DB | ||||
| B、AC2=AD•AB | ||||
C、
| ||||
D、
|

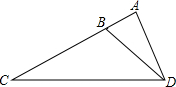 如图,在△ACD中,B为AC上一点,且∠ADB=∠C.
如图,在△ACD中,B为AC上一点,且∠ADB=∠C.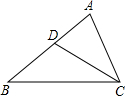 如图,如果∠ACD=∠B,则△ACD∽
如图,如果∠ACD=∠B,则△ACD∽