题目内容
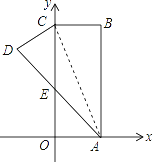
【题目】如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为________.
【答案】(﹣![]() ,
,![]() )
)
【解析】
过D作DF⊥AF于F,根据折叠可以证明△CDE≌△AOE,然后利用全等三角形的性质得到OE=DE,OA=CD=2,设OE=x,那么CE=6-x,DE=x,利用勾股定理即可求出OE的长度,利用已知条件可以证明△AEO∽△ADF,而AD=AB=6,利用相似三角形的性质求出DF、AF的长度,即可得出结果.
如图,过D作DF⊥AF于F,

∵点B的坐标为(2,6),
∴AO=2,AB=6,
根据折叠可知:CD=AO=2,
在△CDE和△AOE中,
 ,
,
∴△CDE≌△AOE(AAS),
∴OE=DE,
设OE=x,则CE=6-x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2,
∴(6-x)2=x2+22,
∴x=![]() ,
,
又∵DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
∵AD=AB=6,
∴AE=CE=6-![]() =
=![]() ,
,
∴![]() ,即
,即![]() ,
,
得:DF=![]() ,AF=
,AF=![]()
∴OF=![]() -2=
-2=![]() ,
,
∴D的坐标为(-![]() ,
,![]() );
);
故答案为:(-![]() ,
,![]() ).
).

【题目】越来越多的人在用微信付款、转账,把微信账户里的钱转到银行卡叫做提现。
自2016年3月l日起,每个微信账户终身享有1000元的免费提现额度,当累计提现金额超过1000元时,累计提现金额超出1000元的部分需支付0.1%的手续费,以后每次提现支付的手续费为提现金额的0.1%.
(1)小明在今天第1次进行了提现,金额为l600元,他需支付手续费_________元;
(2)小亮自2016年3月1日至今,用自己的微信账户共提现3次,3次提现金额和手续费分别如下:
第1次 | 第2次 | 第3次 | |
提现金额(元) | A | b |
|
手续费(元) | 0 | 0.4 | 3.4 |
问:小明3次提现金额各是多少元?
(3)单笔手续费小于0.1元的,按照0.1元收取(即提现不足100元,按照100元收取手续费).小红至今共提现两次,每次提现金额都是整数,共支付手续费2.4元,第一次提现900元。求小红第二次提现金额的范围.