题目内容
【题目】如图,已知四边形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,过
,过![]() 点作
点作![]() ,分别交
,分别交![]() 于点
于点![]() .
.
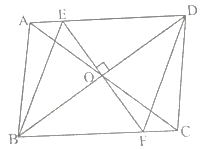
(1)求证: ![]() ;
;
(2)判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)证明见解析;(2)四边形BED是菱形,理由见解析.
【解析】
(1)根据对角线互相平分的四边形是平行四边形,由已知可得四边形ABCD是平行四边形,继而可根据ASA证明ΔAOE≌ΔCOF;
(2)由ΔAOE≌ΔCOF可得OE=OF,再根据OB=OD可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形即可证得四边形BEDF是菱形.
(1)∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
又∵∠AOE=∠COF,OA=OC,
∴△AOE≌△COF(ASA);
(2)四边形BEDF是菱形,理由如下:
∵△AOE≌△COF,
∴OE=OF,
又∵OB=OD,
∴四边形DEBF是平行四边形,
又∵EF⊥BD,
∴平行四边形DEBF是菱形.

练习册系列答案
相关题目
【题目】据了解,火车票价用“![]() ”的方法来确定,已知A站至H站总里程数为1500千米,全程参考价为180元,下表是沿途各站至H站的里程数:
”的方法来确定,已知A站至H站总里程数为1500千米,全程参考价为180元,下表是沿途各站至H站的里程数:
车站名 | A | B | C | D | E | F | G | H |
各站至H站的里程数 | 1500 | 1130 | 910 | 622 | 402 | 219 | 72 | 0 |
例如:要确定从B站至E站的火车票价,其票价为![]() =87.36≈87(元)
=87.36≈87(元)
(1)求A站至F站的火车票价(结果精确到1元);
(2)旅客王大妈去女儿家,上车过两站后拿着火车票问乘务员:我快到了吗?乘务员看到王大妈手中火车票的票价为66元,马上说下一站就到了.请问王大妈是在那一站下车?(写出解答过程)