题目内容
【题目】如图:在数轴上![]() 点表示数
点表示数![]() 点表示数
点表示数![]() 点表示数
点表示数![]() 是最小的正整数,且
是最小的正整数,且![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)若将数轴折叠,使![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数_______表示的点重合;
与数_______表示的点重合;
(3)点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度在数轴上向点
个单位长度的速度在数轴上向点![]() 运动,当点
运动,当点![]() 到达点
到达点![]() 后立即返回,仍然以每秒
后立即返回,仍然以每秒![]() 个单位长度的速度运动至
个单位长度的速度运动至![]() 点停止,设运动时间为
点停止,设运动时间为![]()
①当![]() 时,求点
时,求点![]() 表示的有理数;
表示的有理数;
②当点![]() 表示的有理数与
表示的有理数与![]() 点的距离为
点的距离为![]() 个单位长度时,直接写出所有满足条件的
个单位长度时,直接写出所有满足条件的![]() 值.
值.
![]()
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)10;(3)①2, ②14秒或16秒
;(2)10;(3)①2, ②14秒或16秒
【解析】
(1)根据![]() 可得
可得![]() ,
,![]() ,从而得出a,c的值,再根据b是最小的正整数,得出b的值即可;
,从而得出a,c的值,再根据b是最小的正整数,得出b的值即可;
(2)根据B、C重合,计算出数轴沿着数4对折,再根据点A与数4之间的距离计算出与点A重合的数;
(3)①根据时间计算出点P的运动方向及长度即可;
②对点P的位置进行分类讨论,一是当点P在点B的右侧1个单位时,二是当点P在点B左侧1个单位时,分别计算即可.
解:∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
b是最小的正整数,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]()
(2)∵![]() ,
,
∴若B、C重合,则数轴沿着数4对折,
∴![]() ,
,
∴点A与数10重合,
故答案为:10
(3)∵AC的长度为![]() ,
,
∴当![]() 时,点P已到达点C,并向点A运动了14-9=5(秒)
时,点P已到达点C,并向点A运动了14-9=5(秒)
∴此时点P表示的数为:7-5=2,
∴当![]() 时,点
时,点![]() 表示的有理数是2
表示的有理数是2
②当点P在点B的右侧1个单位时,
∵从A到C需要9秒,所以此时在点B右侧1个单位时,时间为9+(7-1)-1=14(秒)
当点P在点B左侧1个单位时,时间为9+(7-1)+1=16(秒)
故答案为:14秒或16秒.

 阅读快车系列答案
阅读快车系列答案【题目】据了解,火车票价用“![]() ”的方法来确定,已知A站至H站总里程数为1500千米,全程参考价为180元,下表是沿途各站至H站的里程数:
”的方法来确定,已知A站至H站总里程数为1500千米,全程参考价为180元,下表是沿途各站至H站的里程数:
车站名 | A | B | C | D | E | F | G | H |
各站至H站的里程数 | 1500 | 1130 | 910 | 622 | 402 | 219 | 72 | 0 |
例如:要确定从B站至E站的火车票价,其票价为![]() =87.36≈87(元)
=87.36≈87(元)
(1)求A站至F站的火车票价(结果精确到1元);
(2)旅客王大妈去女儿家,上车过两站后拿着火车票问乘务员:我快到了吗?乘务员看到王大妈手中火车票的票价为66元,马上说下一站就到了.请问王大妈是在那一站下车?(写出解答过程)
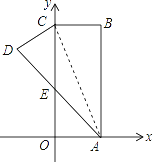
【题目】如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为________.
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?