��Ŀ����
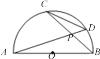
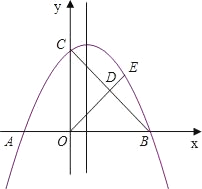
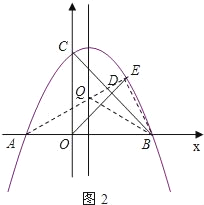
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA��2��OC��3��
��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA��2��OC��3��
��1���������ߵĽ���ʽ��
��2����Rt��OBC�ĸ�OD���ӳ�OD���������ڵ�һ�����ڽ��ڵ�E�����E�����ꣻ
��3������x���Ϸ����������ϣ��Ƿ����һ��P��ʹ�ı���OBEP��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���������ߵĶԳ����ϣ��Ƿ�����ϵ�Q��ʹ����BEQ���ܳ���С�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+3����2����2��2������3���ٴ��ڣ�����1��2�����ڴ��ڣ���
x+3����2����2��2������3���ٴ��ڣ�����1��2�����ڴ��ڣ���![]() ��
��![]() ��
��
��������
��1���ȸ�����֪�����ó�A�㼰C�����꣬���ô���ϵ������������������ߵĽ���ʽ��
��2��y��0���루1����������κ����Ľ���ʽ���ɵij��˺�����x��Ľ������꣬��ODƽ�֡�BOC��֪OE���ڵ�ֱ��Ϊy��x���ٽ��ֱ������������ɵķ����鼴�����E�����ꣻ
��3���ٹ���E��x���ƽ�����������߽�����һ��P������BE��PO����y��2������κ�������ʽ�������P�����꣬�����ɵó��ı���OBEP��ƽ���ı��Σ�
����Q�������߶Գ����ϵ�һ�㣬����QA��QB��QE��BE����QA��QB��֪��BEQ���ܳ�����BE+QA+QE����A��E���������ɵó�ֱ��AE�Ľ���ʽ���ٸ��������ߵĶԳ�����x��![]() �����Q������꣬�����ɵó����ۣ�
�����Q������꣬�����ɵó����ۣ�
�⣺��1����OA��2��
���A����������2��0����
��OC��3��
���C��������0��3����
�߰ѣ���2��0������0��3������y����![]() x2+bx+c����
x2+bx+c����![]() ���
���![]()
�������߽���ʽΪy����![]() x2+
x2+![]() x+3��
x+3��
��2����y��0����y����![]() x2+
x2+![]() x+3��
x+3��
���x1����2��x2��3
���B��������3��0����
��OB��OC��3
��OD��BC��
��ODƽ�֡�BOC
��OE���ڵ�ֱ��Ϊy��x
�ⷽ���� ��
��![]() ��
��![]() ��
��
�ߵ�E�ڵ�һ�����ڣ�
���E��������2��2����
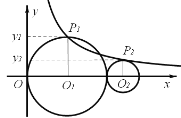
��3���ٴ��ڣ���ͼ1������E��x���ƽ�����������߽�����һ��P������BE��PO��
��y��2����y����![]() x2+
x2+![]() x+3��
x+3��
���x1����1��x2��2
���P����������1��2����
��PE��OB����PE��OB��3��
���ı���OBEP��ƽ���ı��Σ�
����x���Ϸ����������ϣ�����һ��P����1��2����ʹ���ı���OBEP��ƽ���ı��Σ�
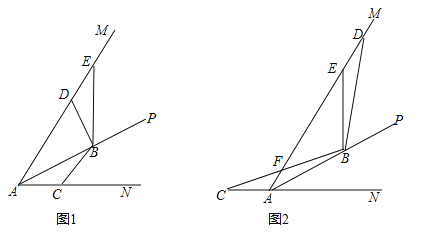
�ڴ��ڣ���ͼ2����Q�������߶Գ����ϵ�һ�㣬����QA��QB��QE��BE��
��QA��QB��
���BEQ���ܳ�����BE+QA+QE��
�֡�BE�ij��Ƕ�ֵ
��A��Q��E��ͬһֱ����ʱ����BEQ���ܳ���С��
��A����2��0����E��2��2���ɵ�ֱ��AE�Ľ���ʽΪy��![]() x+1��
x+1��
�������ߵĶԳ�����x��![]()
���Q��������![]() ��
��![]() ��
��
���������ߵĶԳ����ϣ����ڵ�Q��![]() ��
��![]() ����ʹ����BEQ���ܳ���С��
����ʹ����BEQ���ܳ���С��


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�