Question

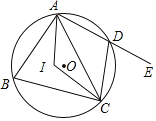
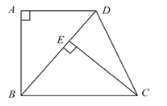
【题目】如图，已知Rt△ABD中，∠A＝90°，将斜边BD绕点B顺时针方向旋转至BC，使BC∥AD，过点C作CE⊥BD于点E．

(1)求证：△ABD≌△ECB；

(2)若∠ABD＝30°，BE=3，求弧CD的长．

Answer 1

【答案】（1）证明见解析；(2)

【解析】

（1）由题意得两个三角形是直角三角形，根据旋转的性质得出BC=BD，由AD∥BC推出∠ADB=∠EBC，即可证明△ABD≌△ECB；
（2）由全等三角形的性质得出AD=BE=3．根据30°角所对的直角边等于斜边的一半得出BD=2AD=6，根据平行线的性质求出∠DBC=60°，再代入弧长计算公式求解即可．

（1）证明：∵∠A=90°,CE⊥BD ∴∠A=∠BEC=90°

∵BC∥AD

∴∠ADB=∠EBC

∵旋转，

∴BD=BC’

∴ △ABD≌△ECB

(2) ∵ △ABD≌△ECB

∴AD=BE=3

∵∠A=90°，∠ABD=30°

∴BD=2AD=6

∵BC ∥ AD

∴∠A+∠ABC=180°

∴∠ABC=90, ∠DBC=60°

.

故答案为：（1）证明见解析；(2) .