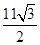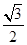题目内容
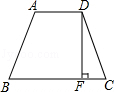
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.
请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)试判断△ABC的形状?请说明理由;
(3)若E为BC中点,F为AD中点.四边形AECF是什么特殊的四边形?请说明理由.

请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)试判断△ABC的形状?请说明理由;
(3)若E为BC中点,F为AD中点.四边形AECF是什么特殊的四边形?请说明理由.

(1)如图

(2)直角三角形,理由见解析
(3)菱形,理由见解析

(2)直角三角形,理由见解析
(3)菱形,理由见解析
试题分析:(1)把BC看成左下角的直角三角形斜边,作一个直角三角形与这个三角形全等,使A与B对应,D与C对应,则AD∥BC;
(2)分别计算三边长度,根据勾股定理的逆定理判断;
(3)根据直角三角形斜边的中线等于斜边的一半证明四边相等判断是菱形.
解:(1)如图,AD为所求作的平行线;

(2)△ABC是直角三角形.
∵AB2=12+22=5;AC2=22+42=20;BC2=32+42=25,
∴BC2=AB2+AC2,
∴△ABC为直角三角形;
(3)四边形AECF为菱形.
由作法知BC平行且对于AD,
∴四边形ABCD是平行四边形,
∴△ACD为直角三角形.
∵F是AD的中点,
∴CF=AF=2.5.
又∵E是BC中点,
∴AE=EC=2.5.
∴AE=EC=CF=AF.
∴四边形AECF是菱形.
点评:此题考查直角三角形的判定和性质、特殊四边形的判定及作图能力,综合性较强.

练习册系列答案
相关题目
 ,请直接写出△ABC的面积.
,请直接写出△ABC的面积.






 ,高DF= .
,高DF= .