题目内容
如图;在等腰梯形ABCD中,AD=2,BC=4,DC= ,高DF= .
,高DF= .
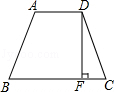
 ,高DF= .
,高DF= .
2
试题分析:先根据等腰梯形的性质求出CF的长,再由勾股定理求出DF的长即可.
解:∵梯形ABCD是等腰梯形,AD=2,BC=4,
∴CF=
 =
= =1,
=1,在Rt△CDF中,
∵CF=1,DC=
 ,
,∴DF=
 =
= =2.
=2.故答案为:2.
点评:本题考查的是等腰梯形的性质及勾股定理,先根据等腰梯形的性质求出CF的长是解答此题的关键.

练习册系列答案
相关题目
题目内容
 ,高DF= .
,高DF= .
 =
= =1,
=1, ,
, =
= =2.
=2.