جâؤ؟ؤعبف
¶¨زه£؛خزأا°رب½اذخ±»ز»±كضذدك·ض³ةµؤء½¸ِب½اذخ½ذ×ِ،°سر؛أب½اذخ،±£®
ذشضت£؛بç¹ûء½¸ِب½اذختا،°سر؛أب½اذخ،±£¬ؤاأ´صâء½¸ِب½اذخµؤأو»دàµب£®
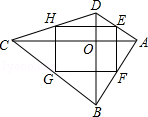
ہي½â£؛بçح¼¢ظ£¬شع،÷ABCضذ£¬CDتاAB±كةدµؤضذدك£¬ؤاأ´،÷ACD؛ح،÷BCDتا،°سر؛أب½اذخ،±£¬²¢ازS،÷ACD=S،÷BCD£®
س¦سأ£؛بçح¼¢ع£¬شع¾طذخABCDضذ£¬AB=4£¬BC=6£¬µمEشعADةد£¬µمFشعBCةد£¬AE=BF£¬AFسëBE½»سعµمO£®
£¨1£©اَض¤£؛،÷AOB؛ح،÷AOEتا،°سر؛أب½اذخ،±£»
£¨2£©ء¬½سOD£¬بô،÷AOE؛ح،÷DOEتا،°سر؛أب½اذخ،±£¬اَثؤ±كذخCDOFµؤأو»£®
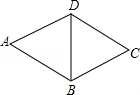
ج½¾؟£؛شع،÷ABCضذ£¬،دA=30،م£¬AB=4£¬µمDشعدك¶خABةد£¬ء¬½سCD£¬،÷ACD؛ح،÷BCDتا،°سر؛أب½اذخ،±£¬½«،÷ACDرطCDثùشعض±دك·صغ£¬µأµ½،÷A،نCD£¬بô،÷A،نCDسë،÷ABCضط؛د²؟·ضµؤأو»µبسع،÷ABCأو»µؤ £¬اëض±½سذ´³ِ،÷ABCµؤأو»£®
£¬اëض±½سذ´³ِ،÷ABCµؤأو»£®

ذشضت£؛بç¹ûء½¸ِب½اذختا،°سر؛أب½اذخ،±£¬ؤاأ´صâء½¸ِب½اذخµؤأو»دàµب£®
ہي½â£؛بçح¼¢ظ£¬شع،÷ABCضذ£¬CDتاAB±كةدµؤضذدك£¬ؤاأ´،÷ACD؛ح،÷BCDتا،°سر؛أب½اذخ،±£¬²¢ازS،÷ACD=S،÷BCD£®
س¦سأ£؛بçح¼¢ع£¬شع¾طذخABCDضذ£¬AB=4£¬BC=6£¬µمEشعADةد£¬µمFشعBCةد£¬AE=BF£¬AFسëBE½»سعµمO£®
£¨1£©اَض¤£؛،÷AOB؛ح،÷AOEتا،°سر؛أب½اذخ،±£»
£¨2£©ء¬½سOD£¬بô،÷AOE؛ح،÷DOEتا،°سر؛أب½اذخ،±£¬اَثؤ±كذخCDOFµؤأو»£®
ج½¾؟£؛شع،÷ABCضذ£¬،دA=30،م£¬AB=4£¬µمDشعدك¶خABةد£¬ء¬½سCD£¬،÷ACD؛ح،÷BCDتا،°سر؛أب½اذخ،±£¬½«،÷ACDرطCDثùشعض±دك·صغ£¬µأµ½،÷A،نCD£¬بô،÷A،نCDسë،÷ABCضط؛د²؟·ضµؤأو»µبسع،÷ABCأو»µؤ
 £¬اëض±½سذ´³ِ،÷ABCµؤأو»£®
£¬اëض±½سذ´³ِ،÷ABCµؤأو»£®
س¦سأ£؛£¨1£©ض¤أ÷¼û½âخِ
£¨2£©،÷ABCµؤأو»تا2»ٍ ،£
،£
£¨2£©،÷ABCµؤأو»تا2»ٍ
 ،£
،£تشجâ·ضخِ£؛س¦سأ£؛£¨1£©ء¬½سEF£¬¸ù¾فز»×é¶ش±كئ½ذذازدàµبµؤثؤ±كذختائ½ذذثؤ±كذخ£¬µأµ½ثؤ±كذخABFEتائ½ذذثؤ±كذخ£¬´س¶ّ¸ù¾فئ½ذذثؤ±كذخµؤذشضتض¤µأOE=OB£¬¼´؟ةض¤µأ،÷AOE؛ح،÷AOBتاسر؛أب½اذخ،£
£¨2£©،÷AOE؛ح،÷DOEتا،°سر؛أب½اذخ،±£¬¼´؟ةµأµ½EتاADµؤضذµم£¬شٍ؟ةزشاَµأ،÷ABE،¢،÷ABFµؤأو»£¬¸ù¾فSثؤ±كذخCDOF=S¾طذخABCD©پ2S،÷ABF¼´؟ةاَ½â،£
½â£؛س¦سأ£؛£¨1£©ض¤أ÷£؛بçح¼£¬ء¬½سEF£¬

،كثؤ±كذخABCDتا¾طذخ£¬
،àAD،خBC،£
،كAE=BF£¬،àثؤ±كذخABFEتائ½ذذثؤ±كذخ،£
،àOE=OB،£،à،÷AOE؛ح،÷AOBتاسر؛أب½اذخ،£
ج½¾؟£؛·ضخھء½ضضاé؟ِ£؛
¢ظبçح¼1£¬ء¬½سA،نB£¬¹B×÷BM،حACسعM£¬

،كS،÷ACD=S،÷BCD£®،àAD=BD=
 AB،£
AB،£،كرطCDصغµA؛حA،نضط؛د£¬،àAD=A،نD=
 AB=
AB= 4=2،£
4=2،£،ك،÷A،نCDسë،÷ABCضط؛د²؟·ضµؤأو»µبسع،÷ABCأو»µؤ
 £¬
£¬،àS،÷DOC=
 S،÷ABC=
S،÷ABC= S،÷BDC=
S،÷BDC= S،÷ADC=
S،÷ADC= S،÷A،نDC،£
S،÷A،نDC،£،àDO=OB£¬A،نO=CO،£،àثؤ±كذخA،نDCBتائ½ذذثؤ±كذخ،£،àBC=A،نD=2،£
،كAB=4£¬،دBAC=30،م£¬،àBM=
 AB=2=BC،£
AB=2=BC،£،àC؛حMضط؛د،£،à،دACB=90،م،£
سة¹´¹ة¶¨ہيµأ£؛
 £¬
£¬،à،÷ABCµؤأو»تا
 ،ءBC،ءAC=
،ءBC،ءAC= ،ء2،ء
،ء2،ء =
= ،£
،£¢عبçح¼2£¬ء¬½سA،نB£¬¹C×÷CQ،حA،نDسعQ£¬

،كS،÷ACD=S،÷BCD£¬،àAD=BD=
 AB،£
AB،£،كرطCDصغµA؛حA،نضط؛د£¬،àAD=A،نD=
 AB
AB 4=2،£
4=2،£،ك،÷A،نCDسë،÷ABCضط؛د²؟·ضµؤأو»µبسع،÷ABCأو»µؤ
 £¬
£¬،àS،÷DOC=
 S،÷ABC=
S،÷ABC= S،÷BDC=
S،÷BDC= S،÷ADC=
S،÷ADC= S،÷A،نDC£¬
S،÷A،نDC£¬،àDO=OA،ن£¬BO=CO،£،àثؤ±كذخA،نDCBتائ½ذذثؤ±كذخ،£
،àBD=A،نC=2،£
،كA،نC=2£¬،دDA،نC=،دBAC=30،م£¬،àCQ=
 A،نC=1£¬
A،نC=1£¬،àS،÷ABC=2S،÷ADC=2S،÷A،نDC=2،ء
 ،ءA،نD،ءCQ=2،ء
،ءA،نD،ءCQ=2،ء ،ء2،ء1=2،£
،ء2،ء1=2،£×غةدثùتِ£¬،÷ABCµؤأو»تا2»ٍ
 ،£
،£
ء·د°²لدµءذ´ً°¸
دà¹طجâؤ؟


 ABCDµؤ¶ش½ادكدཻسعµمO£¬اëؤمجي¼سز»¸ِجُ¼،، ،،£¨ض»جيز»¸ِ¼´؟ة£©£¬ت¹
ABCDµؤ¶ش½ادكدཻسعµمO£¬اëؤمجي¼سز»¸ِجُ¼،، ،،£¨ض»جيز»¸ِ¼´؟ة£©£¬ت¹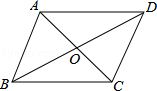

 µؤضµتا £®
µؤضµتا £®