题目内容
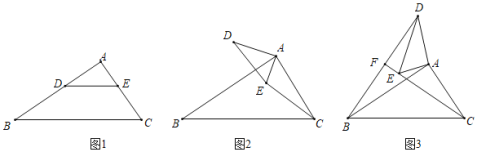
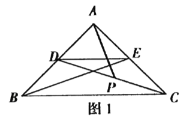
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)观察猜想
图1中,线段![]() 与
与![]() 的数量关系是______,位置关系是________;
的数量关系是______,位置关系是________;
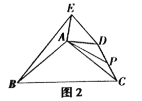
(2)探究证明
把![]() 绕点
绕点![]() 逆时针方向旋转到图2的位置,小航猜想(1)中的结论仍然成立,请你证明小航的猜想;
逆时针方向旋转到图2的位置,小航猜想(1)中的结论仍然成立,请你证明小航的猜想;
(3)拓展延伸
把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)如图1中,设PA交BE于点O.证明△DAC≌△EAB(SAS),结合直角三角形斜边中线的性质即可解决问题. (2)结论成立.如图2中,延长AP到M,使得PM=PA,连接JC.延长PA交BE于O.证明△EAB≌△MCA(SAS),即可解决问题. (3)利用三角形的三边关系求出AM的取值范围,即可解决问题.
解:(1)如图1中,设PA交BE于点O.
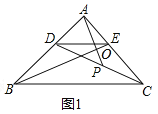
∵AD=AE,AC=AB,∠DAC=∠EAB,
∴△DAC≌△EAB(SAS),
∴BE=CD,∠ACD=∠ABE,
∵∠DAC=90°,DP=PC,
∴PA=![]() CD=PC=PD, ∴PA=
CD=PC=PD, ∴PA=![]() BE.∠C=∠PAE,
BE.∠C=∠PAE,
∵∠CAP+∠BAO=90°, ∴∠ABO+∠BAO=90°,
∴∠AOB=90°, ∴PA⊥BE,
故答案为:![]() ,
,![]()
(2)延长![]() 交
交![]() 于
于![]() 延长
延长![]() 到
到![]() 使
使![]() ,连接
,连接![]() ,
,
则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
又![]() ,
,
![]() ,
,![]()
即![]()
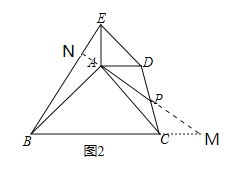
(3)∵A在平面内自由旋转,∴(2)的图形仍然可用,由已知得AC=10,CM=4,
∴10-4≤AM≤10+4,
∴6≤AM≤14,
∵AM=2AP,
∴3≤PA≤7.
∴PA的最大值为7,最小值为3.
所以:![]()

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目