题目内容
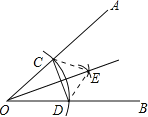
【题目】如图,以![]() 的顶点
的顶点![]() 为圆心,适当长为半径画弧,分别交
为圆心,适当长为半径画弧,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;再分别以
;再分别以![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧在
的长为半径画弧,两弧在![]() 内部交于点
内部交于点![]() ,过点
,过点![]() 作射线
作射线![]() ,连接
,连接![]() ,则下列说法不一定成立的是( )
,则下列说法不一定成立的是( )

A.射线![]() 是
是![]() 的平分线B.
的平分线B.![]() 是等腰三角形
是等腰三角形
C.![]() ,
,![]() 两点关于
两点关于![]() 所在直线对称D.
所在直线对称D.![]() ,
,![]() 两点关于
两点关于![]() 所在直线对称
所在直线对称
【答案】D
【解析】
连接CE、DE,根据作图得到OC=OD、CE=DE,利用SSS证得△EOC≌△EOD从而证明得到射线OE平分∠AOB,判断A正确;根据作图得到OC=OD,判断B正确;根据作图得到OC=OD,由A得到射线OE平分∠AOB,根据等腰三角形三线合一的性质得到OE是CD的垂直平分线,判断C正确;根据作图不能得出CD平分OE,判断D不一定成立.
解:A、连接CE、DE,根据作图得到OC=OD、CE=DE.
∵在△EOC与△EOD中,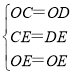 ,
,
∴△EOC≌△EOD(SSS),
∴∠AOE=∠BOE,即射线OE是∠AOB的平分线,正确,不符合题意;
B、根据作图得到OC=OD,
∴△COD是等腰三角形,正确,不符合题意;
C、根据作图得到OC=OD,
又∵射线OE平分∠AOB,
∴OE是CD的垂直平分线,
∴C、D两点关于OE所在直线对称,正确,不符合题意;
D、根据作图不能得出CD平分OE,
∴CD不一定是OE的平分线,
∴O、E两点关于CD所在直线对称不一定成立,符合题意;
故选:D.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案【题目】重庆一中开展了“爱生活爱运动”的活动,以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间,学校在活动之前对八年级同学进行了抽样调査,并根据调査结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如下两幅统计图,请你结合图中所给信息解答下列问题:
(整理数据)

“爱生活·爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
一周体育锻炼时间(小时) | 3 | 4 | 5 | 6 | 7 |
人数 | 3 | 5 | 15 |
| 10 |
(分析数据)
活动之后部分学生体育锻炼时间的统计表
平均数 | 中位数 | 众数 | |
活动之前锻炼时间(小时) | 5 | 5 | 5 |
活动之后锻炼时间(小时) | 5.52 |
|
|
请根据调查信息
(1)补全条形统计图,并计算![]() _____小时,
_____小时,![]() ______小时,
______小时,![]() _____小时;
_____小时;
(2)小亮同学在活动之前与活动之后的这两次调查中,体育锻炼时间均为5小时,根据体育锻炼时间由多到少进行排名统计,请问他在被调查同学中体育锻炼时间排名靠前的是_________(填“活动之前”或“活动之后”),理由是_________________________________.
(3)已知八年级共2000名学生,请估算全年级学生在活动结束后,每周体育锻炼时间至少有6小时的学生人数有多少人?

