题目内容
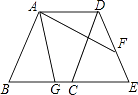
【题目】如图，在平行四边形ABCD中，∠B＝30°，AB＝AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F；点M是边AB的一个三等分点。则△AOE与△BMF的面积比为_________．
【答案】
【解析】连接MF，作AG⊥BC交BC于点G，作MH⊥BC交BC于点H，
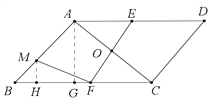
∵AB＝AC，∴∠B=∠ACB=30°，
设AB=AC=6x，则BM=2x，
∴MH=BM·sin30°=x，AG=AB·sin30°=3x，BG=AB·cos30°=3
x，
∵AB=AC，AG⊥BC，∴BG=CG=3x，BC=6x，
∵平行四边形ABCD，∴AD∥BC，OA=OC=3x，
∴∠EAO=∠ACB=30°，∴OE=OA·tan30°=x，AE=
=2x，
∴S△AOE=
OA·OE=
x2，
∵在△AOE和△COF中，
，
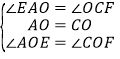∴△AOE≌△COF，
∴AE=CF=2x，
∴BF=6x－2x=4x，
∴S△BMF=BF·MH=2x2，
∴S△AOE∶S△BMF=(x2)∶(2x2)=3∶4.
故答案为3∶4.
练习册系列答案
相关题目
【题目】如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下
：
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
（1）计算上述试验中“4朝下”的频率是多少？
（2）“根据试验结果，投掷一次正四面体，出现2朝下的概率是 
．”的说法正确吗？为什么？
（3）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．
