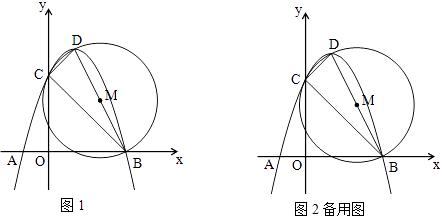��Ŀ����
����Ŀ����֪���������ε����߳�������������������
��ϣ���ļ���ѧ�Һ������������⣬�����������������ۡ�һ���и����˼��㹫ʽ��������ʽS= ![]() ������a��b��c�������ε����߳���p=
������a��b��c�������ε����߳���p= ![]() ��SΪ�����ε����������������֤��
��SΪ�����ε����������������֤��
���磺�ڡ�ABC�У�a=3��b=4��c=5����ô������������������㣺
��a=3��b=4��c=5
��p= ![]() =6
=6
��S= ![]() =
= ![]() =6
=6
��ʵ�ϣ�������֪�����ε����߳�����������������⣬�������ҹ�����ʱ����ѧ���ؾ���������ؾ��ع�ʽ�ȷ��������
��ͼ���ڡ�ABC�У�BC=5��AC=6��AB=9
��1���ú���ʽ���ABC�������
��2�����ABC������Բ�뾶r��
���𰸡�
��1���⣺��BC=5��AC=6��AB=9��
��p= ![]() =
= ![]() =10��
=10��
��S= ![]() =
= ![]() =10
=10 ![]() ��
��
�ʡ�ABC�����10 ![]() ��
��
��2���⣺��S= ![]() r��AC+BC+AB����
r��AC+BC+AB����
��10 ![]() =
= ![]() r��5+6+9����
r��5+6+9����
��ã�r= ![]() ��
��
�ʡ�ABC������Բ�뾶r= ![]() ��
��
��������������Ҫ�����ε�����Բ�����ġ����θ�ʽ��Ӧ�ã��������������ε����������Բ�뾶��Ĺ�ʽ�ǽ���Ĺؼ�����1���ȸ���BC��AC��AB�ij����P���ٴ��뵽��ʽS= ![]() �������S��ֵ����2�����ݹ�ʽS=
�������S��ֵ����2�����ݹ�ʽS= ![]() r��AC+BC+AB��������ɵù���r�ķ��̣��ⷽ�̵�r��ֵ��
r��AC+BC+AB��������ɵù���r�ķ��̣��ⷽ�̵�r��ֵ��

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�