题目内容
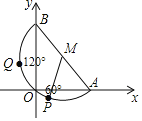
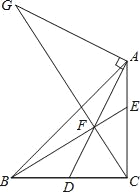
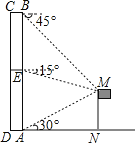
【题目】小甬工作的办公楼（矩形ABCD）前有一旗杆MN，MN⊥DN，旗杆高为12m，在办公楼底A处测得旗杆顶的仰角为30°，在办公楼天台B处测旗杆顶的仰角为45°，在小甬所在办公室楼层E处测得旗杆顶的俯角为15°．
（1）办公楼的高度AB；
（2）求小甬所在办公室楼层的高度AE．
【答案】（1）办公楼的高度AB为（12+12
）m；（2）小甬所在办公室楼层的高度AE为（24﹣24）m
【解析】
（1）过点M作MH⊥AB于点H，可得四边形MNAH是矩形，再根据锐角三角函数即可求出办公楼的高度AB；
（2）过点E作EQ⊥AM于点Q，设AE＝x，则AQ＝xcos60°＝
x，MQ＝EQ＝xsin60°＝
x，由AM＝2MN＝24，列出方程即可求出小甬所在办公室楼层的高度AE．
（1）如图，过点M作MH⊥AB于点H，
∵MN⊥DN，∠BAN＝90°，
∴四边形MNAH是矩形，
∴AH＝MN＝12，
MH∥AN∥BC，
∴∠AMH＝∠MAN＝30°，
在Rt△AMH中，MH＝
＝12，
∵∠BMH＝45°，
∴BH＝MH＝12，
∴AB＝AH+BH＝12+12．
答：办公楼的高度AB为（12+12）m．
（2）过点E作EQ⊥AM于点Q，
由（1）得，∠EAQ＝60°，
∴∠EMQ＝180°﹣∠EAM﹣∠AEM＝180°﹣60°﹣75°＝45°，
设AE＝x，则AQ＝xcos60°＝x，
MQ＝EQ＝xsin60°＝x，
由AM＝2MN＝24，
x＝24，
解得x＝24﹣24（m）．
答：小甬所在办公室楼层的高度AE为（24﹣24）m．
练习册系列答案
相关题目
