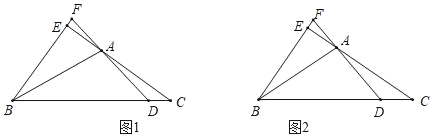
题目内容
【题目】如图,在线段![]() 上有一点
上有一点![]() ,在
,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,且
,且![]() ,
,![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() ,线段
,线段![]() 分别交于点
分别交于点![]() ,对于下列结论:①
,对于下列结论:①![]() ∽
∽![]() ;②
;②![]() ∽
∽![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的是( )
.其中正确的是( )
A. ①②③④B. ①②③C. ①③④D. ①②
【答案】A
【解析】
(1)通过证明![]() ∽
∽![]() ,可判断①;(2)由①
,可判断①;(2)由①![]() ∽
∽![]() ,得
,得![]() ,再证明∠ACE=∠DCB,即可证明②;(3)证明
,再证明∠ACE=∠DCB,即可证明②;(3)证明![]() ∽
∽![]() ,来判定③;(4)通过证明△BDC∽△EAC,△EFB∽△EBA, △EFC∽△ECA, △DFC∽△DCG,来对④进行判断.
,来判定③;(4)通过证明△BDC∽△EAC,△EFB∽△EBA, △EFC∽△ECA, △DFC∽△DCG,来对④进行判断.
解:∵![]() ,
,![]() ,
,![]() ,
,
∴∠ACD=![]() ,∠ECB =∠EBC=
,∠ECB =∠EBC=![]() ,∠ACD=∠EBC.
,∠ACD=∠EBC.
∴DC∥EB
∴![]() ∽
∽![]() ,故①正确;
,故①正确;
∵![]() ∽
∽![]() ,∴
,∴![]()
∵由①得∠ACD=∠ECB,∴∠ACD+∠DCE =∠ECB+∠DCE,即∠ACE=∠DCB,
∴![]() ∽
∽![]() ,故②正确;
,故②正确;
∵![]() ∽
∽![]() ,∴∠CBD=∠FEG,又∵∠FGE=∠CGB,∴
,∴∠CBD=∠FEG,又∵∠FGE=∠CGB,∴![]() ∽
∽![]() ,
,
∴ ![]() , ∴
, ∴ ![]() ,故③正确;
,故③正确;
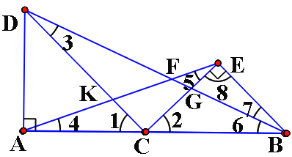
∵∠DAC=∠CEB=90°,AC=AD, BE=CE,
∴△ADC和△BCE是等腰直角三角形,
∴CD=![]() AC=
AC=![]() AD,CB=
AD,CB=![]() CE, ∠1=∠2=45°,∠DCE=90°,∠ACE=∠DCB=180°-45°=135°,
CE, ∠1=∠2=45°,∠DCE=90°,∠ACE=∠DCB=180°-45°=135°,
∴CD:CA=CB:CE=![]() ,
,
∴△BDC∽△EAC
∴∠3=∠4,∠5=∠6,
又∵∠6+∠7=45°,∴∠5+∠7=45°,
又∵∠8=90°,
∴在△EFB中,∠EFB=180°-∠8-(∠5+∠7)=45°,
在△EFB和△BEA中,
∵∠1=∠2=45°,∴∠DCE=90°=∠CEB,
∴DC∥EB,∴∠7=∠3=∠4,∠FEB=∠BEF,
∴△EFB∽△EBA,
∴EB:EF=AE:EB,
又∵∠5=∠5
∴△EFC∽△ECA,
∴∠EFC=∠ECA=180°-∠2=135°,
∴∠BFC=∠EFC-∠EFB=135°-45°=90°.
∴∠DFC=180°-∠CFB=90°=∠DCG
又∵∠3=∠3
∴△DFC∽△DCG,
∴DC:DF=DG:DC,即DC2=DF×DG
又∵CD=![]() AD
AD
∴(![]() AD)2=DF×DG,即2AD2=DF·DG.故④正确.
AD)2=DF×DG,即2AD2=DF·DG.故④正确.
故选:A.

【题目】![]() 朗读者
朗读者![]() 自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级
自开播以来,以其厚重的文化底蕴和感人的人文情怀,感动了数以亿计的观众,岳池县某中学开展“朗读”比赛活动,九年级![]() 、
、![]() 班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩
班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩![]() 满分为100分
满分为100分![]() 如图所示.
如图所示.
平均数 | 中位数 | 众数 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根据图示填写表格;
根据图示填写表格;
![]() 结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
![]() 如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.
如果规定成绩较稳定班级胜出,你认为哪个班级能胜出?说明理由.

【题目】某校两次购买足球和篮球的支出情况如表:
足球(个) | 篮球(个) | 总支出(元) | |
第一次 | 2 | 3 | 310 |
第二次 | 5 | 2 | 500 |
(1)求购买一个足球、一个篮球的花费各需多少元?(请列方程组求解)
(2)学校准备给帮扶的贫困学校送足球、篮球共计60个,恰逢市场对两种球的价格进行了调整,足球售价提高了10%,篮球售价降低了10%,如果要求一次性购得这批球的总费用不超过4000元,那么最多可以购买多少个足球?