Question

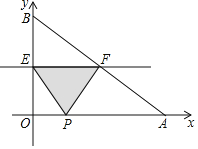
【题目】如图，在平面直角坐标系中，A、B两点的坐标分别为（20，0）和（0，15），动点P从点A出发在线段AO上以每秒2cm的速度向原点O运动，动直线EF从x轴开始以每秒lcm的速度向上平行移动（即EF∥x轴），分别与y轴、线段AB交于点E、F，连接EP、FP，设动点P与动直线EF同时出发，运动时间为t秒．

（1）求t=9时，△PEF的面积；

（2）直线EF、点P在运动过程中，是否存在这样的t使得△PEF的面积等于40cm2？若存在，请求出此时t的值；若不存在，请说明理由；

（3）当t为何值时，△EOP与△BOA相似．

Answer 1

【答案】（1）36cm2；（2）不存在；（3）t=6或t=.

【解析】

（1）由于EF∥x轴，则S△PEF=EFOE．t=9时，OE=9，关键是求EF．易证△BEF∽△BOA，则=，从而求出EF的长度，得出△PEF的面积；

（2）假设存在这样的t，使得△PEF的面积等于40cm2，则根据面积公式列出方程，由根的判别式进行判断，得出结论；

（3）如果△EOP与△BOA相似，由于∠EOP=∠BOA=90°，则只能点O与点O对应，然后分两种情况分别讨论：①点P与点A对应；②点P与点B对应．

解：（1）∵EF∥OA，

∴∠BEF=∠BOA

又∵∠B=∠B，

∴△BEF∽△BOA，

∴=，

当t=9时，OE=9，OA=20，OB=15，

∴EF==8，

∴S△PEF=EFOE=×8×9=36（cm2）；

（2）∵△BEF∽△BOA，

∴EF===（15-t），

∴×（15-t）×t=40，

整理，得t2-15t+60=0，

∵△=152-4×1×60＜0，

∴方程没有实数根．

∴不存在使得△PEF的面积等于40cm2的t值；

（3）当∠EPO=∠BAO时，△EOP∽△BOA，

∴=，即=，

解得t=6；

当∠EPO=∠ABO时，△EOP∽△AOB，

∴=，即=，

解得t=．

∴当t=6或t=时，△EOP与△BOA相似．