题目内容
【题目】三角形两边长分别是![]() 和
和![]() ,第三边的长是一元二次方程
,第三边的长是一元二次方程![]() 的一个实数根,则此三角形的外接圆半径为________.
的一个实数根,则此三角形的外接圆半径为________.
【答案】![]() 或
或![]()
【解析】
先解方程,根据三角形的三边关系可知,方程的两个解都能和已知的两边构建成新的三角形,因此求此三角形的外接圆半径时,有两种情况:第一种情况:三边分别为6、8、10,是直角三角形,所以其斜边就是外接圆的直径,第二种情况:三边分别为6、6、8,等腰三角形,其外接圆的圆心是任意两边垂直平分线的交点,确定其圆心,利用勾股定理列方程可求其半径.
x216x+60=0,
(x10)(x6)=0,
x=10或6,
当第三边为10时,因为![]()
∴此三角形是直角三角形,如图1,
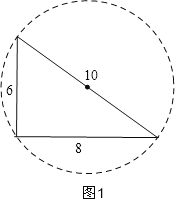
此三角形的外接圆的直径为最大边10,
则此三角形的外接圆半径为5,
当第三边为6时,如图2,
过A作AD⊥BC,垂足为D,作AC的垂直平分线EF,交AC于E,交AD于F,则AF=FC,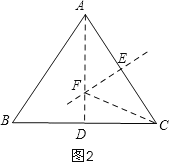
∵AB=AC=6,
∴![]()
∴AD是BC的垂直平分线,
∴F是△ABC外接圆的圆心,FC为外接圆的半径,
由勾股定理得:![]()
设FC=x,则AF=x,![]()
由勾股定理得:![]()
x=![]() ,
,
综上所述,则此三角形的外接圆半径为5或![]() .
.
故答案为:![]() 或
或![]()

练习册系列答案
相关题目