Question

【题目】如图，AB是⊙O的直径，点C在BA的延长线上，CA=AO，点D在⊙O上，∠ABD=30°．

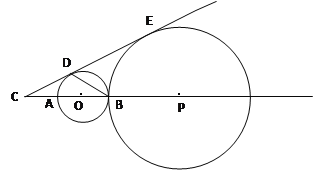
⑴求证：CD是⊙O的切线；

⑵若点P在直线AB上，⊙P与⊙O外切于点B，与直线CD相切于点E，设⊙O与⊙P的半径分别为r与R，求的值．

Answer 1

【答案】（1）证明：连结OD、DA

∵AB是⊙O的直径，∴∠BDA=90°

又∠ABD=30°，∴AD=AB=OA

又AC=AO，∴∠ODC=90°

∴CD切⊙O于点D

（2）方法一：连结PE，由（1）知∠DAB=60°，又AD=AC

∴∠C=30°

又∵DE切⊙P于E，∴PE⊥CE

∴PE=CP

又PE=BP=R，CA=AO=OB=r

∴3r=R，即

方法二：连结PE，

又∵DE切⊙P于E，∴PE⊥CE

∴OD∥PE

∴=

即，∴

【解析】

（1）欲证：CD是⊙O的切线，只要转化为证明∠ODC=90°即可；

（2）连接PE，易证，又PE=BP=R，CA=AO=OB=r，即可得到结果．